अब तक का सबसे बड़ा 'पोंजी स्कीम'

वालस्ट्रीट में फ्रौड़ का इतिहास बड़ा लंबा रहा है. इतनी सारी विफलताएं है कि गिनना मुश्किल है.

हर मामले में कहानी एक जैसी ही होती है... एक घाटे को बचाने के लिए, उसे छिपाने के लिए नए निवेश करते जाओ और तब तक करते जाओ जब तक पानी सर के ऊपर ना निकल जाए. छोटे-मोटे स्कैंडल तो इस धंधे का हिस्सा लगने लगे हैं. पर जब 'अब तक का सबसे बड़ा' टैग लग जाता है तो सच में कुछ बड़ा होता है. और अगर वालस्ट्रीट का अब तक का सबसे बड़ा कुछ है मतलब सच में कुछ बड़ा तो होगा ही !

११ दिसम्बर को नैस्डैक के पूर्व चेयरमैन मैडोफ़ को ५० अरब डॉलर के फ्रौड़ के आरोप में गिरफ्तार किया गया। वालस्ट्रीट की जानी-मानी हस्तियों में से एक मैडोफ़ पर लगा ये आरोप एक अकेले व्यक्ति पर लगा सबसे बड़ा फ्रौड़ का आरोप है। उन्होंने ख़ुद ऍफ़बीआई के सामने ये स्वीकार किया की बर्नार्ड एल मैडोफ़ सेक्युरिटीस् का निवेश एक बड़ा पोंजी स्कीम था ! ये लाईने आप सीधे अंग्रेजी में ही पढिये:

On Dec. 10, 2008, Madoff informed the Senior Employees, in substance, that his investment advisory business was a fraud. Madoff stated that he was "finished," that he had "absolutely nothing," that "it's all just one big lie," and that it was "basically, a giant Ponzi scheme. Madoff stated that the business was insolvent, and that it had been for years. Madoff also stated that he estimated the losses from this fraud to be at least approximately $50 billion.

बर्नार्ड एल मैडोफ़ सेक्युरिटीस् की वेबसाइट पर:

'The Owner's Name is on the Door'

In an era of faceless organizations owned by other equally faceless organizations, Bernard L. Madoff Investment Securities LLC harks back to an earlier era in the financial world: The owner's name is on the door. Clients know that Bernard Madoff has a personal interest in maintaining the unblemished record of value, fair-dealing, and high ethical standards that has always been the firm's hallmark.

Bernard L. Madoff founded the investment firm that bears his name in 1960, soon after leaving law school. His brother, Peter B. Madoff, graduated from law school and joined the firm in 1970. While building the firm into a significant force in the securities industry, they have both been deeply involved in leading the dramatic transformation that has been underway in US securities trading.

और ११ दिसम्बर तक तो सब यही मानते थे... अक्सर यही होता है. वालस्ट्रीट में जो सबसे बड़ा स्टार होता है वही गड़बड़ करता है ! पुरा आप यहाँ जाकर पढ़ सकते हैं.

फिलहाल खबरें आ ही रही हैं... बड़े-बड़े अरबपति और कुछ बड़े बैंक के पैसे (सॉरी डॉलर) साफ़ हो गए. प्रभावित लोगों और संस्थाओं की एक सूची विकिपीडिया पर है... जिसमें अभी और भी नाम आएंगे ! मैडोफ़ को फिलहाल १ करोड़ डॉलर की जमानत पर रिहा कर दिया गया है. मामला चलेगा, जेल भी होगा... वो सब तो ठीक पर ये 'पोंजी स्कीम' क्या है?

पोंजी ऐसे फ्रौड़ निवेश स्कीम को कहते हैं जो बहुत ज्यादा लाभ देता है. पर निवेशकों का लाभ किसी सफल बिजनेस या उत्कृष्ट निवेश से ना होकर दुसरें निवेशकों के पैसे से आता है ! १९२० में चार्ल्स पोंजी के नाम पर इसे पोंजी स्कीम कहा गया. वैसे पोंजी ख़ुद स्कीम के आविष्कारक नहीं थे लेकिन उन्होंने बड़े स्केल पे किया तो उनके नाम पर ही चल निकला. ये घटना सीधे पोंजी स्कीम तो नहीं है पर उसी का एक रूप है. 'जब घाटा होने लगे तो भी झूठ बोलकर निवेशकों से पैसे लेते रहना और ये सोचना की कल को पैसे बन जायेंगे !' यही मुख्य कारण होता है अधिकतर पोंजी स्कीम्स में.

वाल स्ट्रीट जर्नल ने इस पूरे घटना क्रम की कवरेज की है. और अब तक के बड़े पोंजी घटनाओं पर एक ग्राफिक्स भी यहाँ है.

और हाँ ऍफ़बीआई का ओरिजनल कम्प्लेन डोक्युमेंट देखना हो तो यहाँ देख लीजिये.

कम से कम ऐसे निवेश से सावधान रहिएगा. कई करोड़पति-अरबपति पूंजी से पोंजीपति हो गए इस घटना में !

--
मुझे तो इसी बात की खुशी है की जो परीक्षा आजकल दे रहा हूँ उसका चौथा पेपर कम्प्लीट कर लिया. उसमें ऐसे ही फ्रौड़ और कंपनियों की विफलताएं पढ़नी होती है... रोचक तो बहुत होती है लेकिन इस साल इतनी ज्यादा केस-स्टडीज हो गई की इन सब को जोड़ दिया जाय तो पढ़ते-पढ़ते... !

अगर वित्त अर्थ से जुड़ी खबरें आप पढ़ते हैं तो मैं रीडर में बहुत कुछ शेयर करता हूँ. आप यहाँ देख सकते हैं.

गणित के साथ ऐसी कहानियो को भी ठेलने का मन था (है) लेकिन आजकल तो गणित भी बंद है !

~Abhishek Ojha~

ईटो कियोशी

पॉल क्रुगमन के ब्लॉग से पता चला की ईटो कियोशी नही रहे। प्रायिकता सिद्धांत (Probability Theory) और आकस्मिकता (Randomness) पर उनका काम जो ईटो कलन (Ito Calculus) के नाम से जाना जाता है. गणितीय वित्त में बहुत ज्यादा इस्तेमाल होता है। याद है जब पहली बार ईटो लेमा (Ito's Lemma) वित्तीय गणित की कक्षा में सुना था... उसके बाद अगली तीन कक्षाओं तक कुछ हवा नहीं लगी थी। ये कोर्स १० वें सेमेस्टर में किया था मतलब ४ साल तक गणित पढने के बाद भी पहली बार में ये सिद्धांत और इसका इस्तेमाल समझ नहीं आया था। फिर ऐसे नाम इतनी जल्दी कोई कैसे भूल सकता है. अब जब कभी साक्षात्कार लेता हूँ और अगर किसी ने वित्तीय गणित के बारे में पढ़ा हो तो उससे एक बार ईटो लेमा और फेनिमन कक (Feynman Kac) में से एक तो पूछ ही लेता हूँ।

१९१५ में जन्में इस जापानी गणितज्ञ ने पिछले दोनों १० नवम्बर को आखिरी साँस ली। २००६ में पहले गॉस पुरस्कार से सम्मानित इस गणितज्ञ द्बारा विकसित सिद्धांत वित्त के अलावा जीव विज्ञान (Biology) और भौतिकशास्त्र (Physics) में भी उपयोगी साबित हुए हैं। पिछले महीने ही उन्हें जापानी आर्डर ऑफ़ कल्चर पुरस्कार से नवाजा गया था। वित्त और खासकर डेरिवेटिव ट्रेडिंग में उनके सिद्धांतों के उपयोग के चलते उन्हें 'Most Famous Japanese in WallStreet' की उपाधि से भी जाना जाता है। स्टोकास्टिक डिफ़ेरेन्शियल समीकरणों (Stochastic Differential Equations) पर उनके काम ब्लैक-शोल्स मॉडल (Black Scholes Model) तक पहुचने में मदद करते हैं। अब जो वित्तीय अभियांत्रिकी (Financial Engineering) का नाम भी सुनते हैं वो ब्लैक-शोल्स तो जानते ही हैं।

एमआईटी के प्रोफेसर डैनियल स्ट्रूक ने कहा: 'सबको पता है की ईटो के काम से कई बातो की जानकारी हुई जो पहले अनजान थी।'

श्रद्धांजली इस महान गणितज्ञ को !

--
पाल क्रुगमैन के ब्लॉग पर पढने के बाद सोचा की इस पर कुछ लिखा जाय। कल से पढ़ाई के लिए छुट्टी पर हूँ (हमारी कम्पनी पढने के लिए भी छुट्टी देती है)... और परसों रात से ही टाईम्स नाऊ देख रहा हूँ... मैं तो फिर भी २ घंटे बिजली गई तो ४ घंटे सो गया लेकिन कमांडो बिना सोये लगे हुए हैं... और टाईम्स नाऊ पर अर्नब ! बिना एडवटिज्मेन्ट, कमाल की कवरेज ! टीवी पर न्यूज़ नहीं देखता पर इस बार टीवी बंद करने की इच्छा नहीं हो रही है... दिमाग शून्य हो गया है ! इससे ज्यादा लिखने की क्षमता नहीं.

नरीमन भवन में शायद कार्यवाही ख़त्म हो गई है...

~Abhishek Ojha~

गणित से भय: यूरोप की देन ?

गणित और भय में चोली-दामन का रिश्ता है और हाल ही में मुझे रंजनाजी के सौजन्य से पता चला की ये यूरोपीय विचारधारा की देन है. रंजनाजी ने कुछ दस दिनों पहले मुझे ये अखबार का टुकडा स्कैन कर के भेजा. अब उन्हें लगा की मुझे  इस पर कुछ लिखना चाहिए... अब मेरे दिमाग में तो यही आया 'अब आगे से किसी को गणित से डरने के जरुरत नहीं...  ये गणित से डरना फिरंगियों की सोच से प्रभावित है.' लेकिन इससे कोई फायदा है क्या, किसी की भी विचारधारा हो ?  जैसे बच्चे को कितना भी समझा लो कि बेटा भूत-वूत कुछ नहीं होता, सब वहम है... पर वो तो डरेगा ही ! वैसे ही क्या फर्क पड़ता है कि किसने डराने वाला गणित बनाया... अब ये वहम मिटाना आसन नहीं.

खैर बात इस ख़बर की... मुझे पढने के बाद यही लगा कि ये प्रो राजू की पुस्तक 'कल्चरल फाउण्डेशनस ऑफ़ मैथेमेटिक्स' में कही गई बात है. इसका स्रोत ढूंढने की  थोडी कोशिश भी की... गणित भले ही यूरोपीय सोच की देन हो ना हो... ये ख़बर इन बातों पर आधारित है: प्रो राजू की पुस्तक में यह कहा गया है की कलन (Calculus) जिसके लिए कहा जाता है कि न्यूटन (Newton) और लिबनिज (leibnitz) दोनों ने स्वतंत्र रूप से विकसित किया, दरअसल भारत की देन  है. कलन के कई प्रमुख सिद्धांत आर्यभट, भास्कर, नीलकंठ, शंकर वारियार जैसे गणितज्ञों के कई खगोलीय और गणितीय कामों में पाये जाते हैं जिसे मैटियो रिक्की नामक जेसुइट द्वारा कोचीन से यूरोप ले जाया गया. अन्यत्र प्रो राजू कहते हैं की प्राचीन भारतीय और यूरोपीय गणितीय सोच में बहुत अन्तर है. भारतीय गणित जहाँ व्यवहारिक था वहीँ यूरोप ने इसे धर्म से जोड़ दिया. भारतीय 'प्रमाण' में जहाँ 'लगभग' की मान्यता थी वहीँ यूरोप के 'प्रूफ़' में इसे परफेक्ट बना दिया गया. प्लेटो ने जोड़-घटाव (व्यवहारिक गणित/Applied Mathematics) वाले गणित को प्रूफ़ (प्रूफ़ पर आधारित शुद्ध गणित/Proof based Pure Mathematics)  वाले गणित से नीचे माना और यह मान्यता आज तक शिक्षाविदों में चली आ रही है कि शुद्ध गणित व्यवहारिक गणित से ज्यादा श्रेष्ठ है. जबकि भारत में कभी भी ऐसा विवाद नहीं रहा... प्राचीन भारतीय गणित केवल पढने के लिए कभी नहीं था बल्कि हमेशा ही वो किसी व्यवहारिक उपयोग को लेकर रहा है. जबकि शुद्ध गणित जो यूरोपीय सोच का नतीजा था वो केवल पढने के लिए रहा… अर्थात वास्तविकता से दूर.

गणित के इस रूप के भारत से यूरोप जाने और विकृत होने के बारे में प्रो राजू कहते हैं की यूरोप में नौसंचालन के लिए की जाने वाली शुरूआती गणनाओं में कई गलतियाँ थी. जिससे समस्याएं भी होती थी और नौसंचालन में सुविधा के लिए किए जाने वाले आविष्कारों के लिए कई यूरोपीय राज्यों ने आकर्षक पुरस्कारों की घोषणा कर रखी थी. इनके सुधार के लिए भारतीय गणित और पंचांगों को जेसुइट केरल से यूरोप ले गए. केरल उस समय शिक्षा और गणित का केन्द्र हुआ करता था क्योंकि विजयनगर राज्य की प्रभुता के कारण यह उत्तरी हमलों से एकदम सुरक्षित था. जेसुइट समुदाय के लोगों का स्थानीय लोगों से घुल-मिल कर रहना था और उन्हें भाषा की दिक्कत भी नहीं होती थी. इस तरह कई त्रिकोणमितीय अनुपातों को निकालने की विधि सहित पंचांगों और अन्य खगोलीय तथा  गणितीय अध्ययनों में उपयुक्त सिद्धांत यूरोप पहुच गए. वहाँ आध्यात्म विद्या (Theology) से जुड़ जाने के कारण इसमें अमूर्तता (Abstraction) आई और फिर इसका रूप कठिन होता गया और भय का रूप लेता चला गया....

अगर व्यवहारिक गणित और शुद्ध गणित क्या है ये जानने की इच्छा हो तो ये देख लें:

व्यावहारिक गणित (बातें गणित की... भाग III)

शुद्ध गणित (बातें गणित की... भाग II)

--
ये प्रो राजू के विचार हैं और इनमें से कई विचारों पर मेरी व्यक्तिगत सहमती नहीं है. उनके कुछ लेख और विचार पढने के बाद उनसे भारी असहमति लगती है. उस पर उनकी किताब पढने के बाद कभी चर्चा होगी.

फिलहाल ये गणित से डरना अपना काम नहीं ये यूरोपीय विचार धारा है. गाँधी बाबा को ये बात पता होती तो स्वदेशी आन्दोलन का हिस्सा बन गया होता "हम गणित से नहीं डरेंगे क्योंकि ये यूरोपीय विचारधारा है" और चरखे के साथ-साथ वैदिक गणित और लीलावती जैसी पुस्तकें भी होती ! खैर अभी भी स्वदेशी आन्दोलन चलाने वाले लोग हैं उन तक बात पहुचाने की जरुरत है. :-)

रंजनाजी को धन्यवाद !

~Abhishek Ojha~

दिवाली पर गणितीय रंगोली !

दीपावली की हार्दिक शुभकामनायें ! गणित की रंगोली और गणित के ही पटाखों के साथ...

पहले कुछ रंगोली:

इन खुबसूरत रंगोलियों को किसी कलाकार ने नहीं बनाया है. ये गणित के कुछ फलन हैं जिन्हें कंप्यूटर की मदद से बनाया गया है. इन चित्रों को फ्रैक्टल कहते हैं. ये क्या होते हैं और कैसे बनते हैं... ये जानते हैं दिवाली के बाद. अभी आप इतना ही जानिए ये पूर्ण रूप से गणित के सूत्र ही हैं और कुछ नहीं... ये कैनवास पर बने गई किसी कलाकार की कल्पना नहीं गणितज्ञों के दिमाग की उपज है.

और फिर जाते-जाते एक फ्रैक्टल पटाखा:

सारे फ्रैक्टल केओसप्रो से बनाए गए हैं.

~Abhishek Ojha~

इश्क से गिरे, गणित पे अटके ...

फर्मैट के अन्तिम प्रमेय की श्रृंखला में कई बातें आई थी... अब इतने लंबे समय तक अगर कोई सवाल अनसुलझा रहे तो कहानियाँ तो होगी ही। कई सारे पुरस्कार भी रखे गए थे...

एक ऐसा ही पुरस्कार रखा था जर्मनी के डॉक्टर उद्योगपति पॉल फ्रेडरिक वोल्फ्केल (Paul Friedrich Wolfskehl) ने। यूँ तो पेशे से डॉक्टर थे पर एक बीमारी की वजह से ये पेशा छोड़ना पड़ा। और फिर गणित में रूचि हो गई... पर इन्होने अपनी कमाई के एक बड़े हिस्से को फर्मैट के अन्तिम प्रमेय पर पुरस्कार देने की जो घोषणा की उसके पीछे गणित में उपजी रूचि से ज्यादा इश्क का हाथ था।

कहते हैं की वोल्फ्केल को इश्क में धोखा मिला (जो की अक्सर मिलता है...) और फिर वो ऐसे टूटे की उन्होंने आत्महत्या की सोंची (अक्सर हो न हो ये भी होता ही है)।

पर इसी बीच वो पुस्तकालय चले गए और गणित की एक किताब में खो गए... उन्हें फर्मैट के अन्तिम प्रमेय पर लिखे गए क्युम्मर (Kummer) के एक पेपर में ऐसा लगा कि कुछ गड़बड़ है। दरअसल इस पेपर में क्युम्मर ने कौशी (Cauchy) के काम में गलती निकाली थी, जिससे यह साबित हुआ था कि कौशी का प्रूफ़ ग़लत है. वोल्फ्केल को लगा कि क्युम्मर ही ग़लत है और कौशी अभी भी सही है... हालाँकि उनको जो लगा वो बात तो नहीं थी पर इसमें वो ऐसे उलझे कि आत्महत्या का विचार ही त्याग दिया। और चूँकि ये सारे पेपर फर्मैट के अन्तिम प्रमेय से सम्बंधित थे तो उन्हें लगा की कहीं न कहीं उनकी जान बचाने में इस प्रमेय का भी हाथ हैं।

अब उनकी प्रेमिका कौन थी ये तो कोई नहीं जानता पर ये कहानी उस प्रेमिका का नाम लिए बिना कई किताबों में छपी... और कारण भले थोड़े अलग हो पर कहानी ऐसी ही होती है... कुछ लोग ऐसा कारण भी देते हैं: उन्हें अपनी प्रेमिका की बेवफाई के बाद फिर से दुबारा प्यार नहीं हो पाया और वो नहीं चाहते थे की उनके बाद ये पैसा उनकी बीवी को मिले ! और पुराना प्यार भुलाने में प्रमेय ने मदद तो की ही थी... तो अगर पैसे कहीं लगाना ही है तो इसी काम में क्यों नहीं ! और इस तरह उन्होंने अपनी कमाई के १ लाख मार्क (आज के १० लाख पौंड) उस आदमी को देने की घोषणा कर दी जो पहली बार इस प्रमेय को सही या ग़लत साबित करेगा।

उनकी मृत्यु के करीब ९० साल बाद अंततः ये पुरस्कार एंड्र्यू वाइल्स को १९९७ में दिया गया। इतिहास में एक बार दिए गए इस पुरस्कार के बारे में और जानकारी के लिए यहाँ जाकर पढ़ें.

फर्मैट की श्रृंखला के अन्य लेख:
१. गणित के महानतम सवाल का रोचक इतिहास (बातें गणित की... भाग VII)
२. एक अनसुलझे सवाल से मिली मदद (बातें गणित की... भाग VIII)
३. सात साल में बना १००० पन्नों का हल (बातें गणित की... भाग IX)
४. एंड्र्यू वाइल्स, फील्ड्स मेडल और एक महिला गणितज्ञ (बातें गणित की... भाग X)
५. एक महिला गणितज्ञ के गणित प्रेम की दुखद कहानी ! (बातें गणित की... भाग XI)

गणित द्बारा जान बचाने वाली एक और कहानी:
गणित ने बचाई जान (बातें गणित की भाग... IV)

~Abhishek Ojha~

सुनहरा अनुपात... और सब कुछ !

पिछले कुछ पोस्ट से... यहाँ पाया जाता है, वहां पाया जाता है ! आज समाप्त ही कर देते है... हर जगह पाया जाता है ! कम से कम हर खुबसूरत चीज में....

हर जगह पाया जाने वाला यह दैविक अनुपात प्रकृति में भी बहुतायत में पाया जाता है... घोघा शंख और मानव शरीर में इसकी उपस्थिति तो हम देख ही चुके हैं. फूलों और पत्तियों की बनावट में भी बड़ी आसानी से इसे पाया जाता है. सूर्यमुखी का फूल सबसे बड़ा उदहारण है जिनमें कई सारे गोल्डन स्पयाराल्स होते हैं. आज मुझे लगता है की लिखने से बेहतर है की कुछ लाजवाब लिंक दे दिए जाएँ... इतनी मेहनत से किसी ने ये साईट तैयार की है... और मेरा विश्वास है की एक बार देखने के बाद आपको आश्चर्य जरूर होगा... कहाँ नहीं पाया जाता ये अनुपात?

मानव शरीर में इसकी उपस्थिति: (सारे तस्वीर इसी लिंक से)

इस लिंक पर आप इन से सम्बंधित चित्र और व्याख्या देख सकते हैं:

- सुन्दरता और चहरे के माप के अनुपात

- मानव शरीर के विभिन्न अंगों का अनुपात

- तर्जनी अंगुली के विभिन्न हिस्सों में इस अनुपात और फिबोनाच्ची की उपस्थिति. (चित्र में)

- कान, आँख, हाथ तथा दांत जैसे अंगों में इसकी उपस्थिति.

- डीएनए और ईसीजी में उपस्थिति

- कुछ मछली, कीडे, चिडिया... इत्यादि में

प्रकृति में: अब ये स्लाइड शो देखिये... गैलेक्सी से लेकर, फूलों, फलों और पत्तियों में आप देख पायेंगे !

वैसे तो हम कला और स्थापत्य कला में इसकी उपस्थिति देख चुके हैं पर आज ये लिंक इतना कमाल का मिल गया की इसका लिंक दिए बिना नहीं रहा गया. तो ये भी देख लीजिये.

मानव शरीर और प्रकृति पर ये स्लाइड शो मिल जाने के बाद लिखने की कुछ गुन्जाईस ही नहीं बचती. अब संगीत में तो वायलिन की संरचना ही देख लीजिये. ऐसा पाया गया है कि जो संगीत सुनने के कक्ष सबसे अच्छे होते हैं उनके माप का अनुपात इस अनुपात के काफ़ी करीब होता हैं. संगीत के क्रम में जो अंतराल होते हैं उनमें इसकी उपस्थिति होती है... मुझे संगीत का कुछ ज्ञान नहीं पर ये बातें शायद आपको समझ में आए.

अब जाते-जाते सुन्दरता... ऐसे प्रयोग किए गए और निष्कर्ष निकाला गया कि जिनके चहरे में ये अनुपात होता है वो ज्यादा आकर्षक होते हैं. परफेक्ट फेस की भी मोडेलिंग की गई. इस पर भी ये लिंक देख आइये. जाते-जाते एक बार और अनुरोध करना चाहूँगा की ये सारे लिंक देख लें... निराशा नहीं होगी. सुनहरे अनुपात की श्रृंखला को अगर इन लिंकों के साथ ख़त्म न किया जाय तो चलती ही रहेगी.

इसके बाद भी किसी को जिज्ञासा हो या जिज्ञासा पैदा हो गई हो... तो अपना ईमेल दे दीजिये पूरी किताब पड़ी है मेरे पास... जिनमें दो २५० पन्नों से ज्यादा की हैं !

इस श्रृंखला की पिछली कड़ियाँ:

सुनहरा अनुपात और स्थापत्यकला

सुनहरा अनुपात और चित्रकारी

सुनहरा आयत, अनुपात और फिबोनाच्ची

कलाकारों और वास्तुशिल्पियों की पसंद: सुनहरा अनुपात

उत्कृष्ट लिंक:

http://milan.milanovic.org/math/

http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html

~Abhishek Ojha~

और अगर कभी फुर्सत मिले तो ये विडियो भी... थोड़ा समय लगेगा पर है कमाल का !

सुनहरा अनुपात और स्थापत्यकला

सुनहरे अनुपात की स्थापत्य कला में उपस्थिति बहुत पुरानी है.... जैसे चित्रकारी में मोनालिसा और लियोनार्दो दा विन्ची की कृतियाँ सबसे पहले दिमाग में आ जाती हैं वैसे ही स्थापत्य कला के प्राचीन अनूठे नमूनों की बात करें तो पिरामिड ही दिमाग में आते हैं। पिरामिड का निर्माण क्यों और कैसे हुआ ये तो आप सब जानते ही हैं... पर अगर गौर से देखा जाय तो सूक्ष्म से बड़े स्तर तक कई वैज्ञानिक तथ्य इनमें छुपे हुए हैं। ठीक दा विन्ची के चित्रों की तरह। 

---

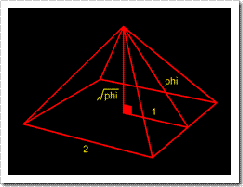अगर पिरामिड का अनुप्रस्थ काट देखें तो यह ऐसा दीखता है।  चित्र में जो phi है वो वही सुनहरा  अनुपात है (१.६१८...). यानी पिरामिड की तिरछी ऊंचाई और जमीन के केन्द्र से उसकी दूरी का  अनुपात. पिरामिड से निकाला गया यह यह अनुपात सुनहरे अनुपात से दशमलव के ४ अंको तक मिलता है। अगर केन्द्र से यह दूरी १ ले लें तो पिरामिड की ऊंचाई phi के वर्गमूल के बराबर हो जाती है। और इस चित्र में अगर आप थोड़ा और गणित लगा लें तो पायेंगे की  झुकी हुई सतह का क्षेत्रफल भी phi ही आ जाता है। फ़राओ निर्मित महान गीज़ा के पिरामिड में यह अनुपात सबसे सटीक मिलता है.

---

आगे बढ़ते हैं पेरिस की तरफ़... यहाँ पर  नोट्रेडेम (Notre Dame) नाम से प्रख्यात कैथेडरल है. यह कैथेडरल फ्रांसीसी स्थापत्यकला के सबसे प्रसिद्द इमारतों में से एक है. फ्रांसीसी क्रांति के समय इसे भारी क्षति पहुँची थी पर पिछली शताब्दी में फिर से इसका जीर्णोद्धार कर पहले की अवस्था में ले आया गया (काश अपने यहाँ भी ऐतिहासिक भवनों के साथ ऐसा हो पाता). १२वीं सदी में निर्मित स्थापत्य कला के इस अद्भुत नमूने के जगमगाते चित्र के साथ ये चित्र  भी देख लीजिये, इस चित्र में अनुपात को रेखांकित किया गया है. । तो अगली बात जब आप पेरिस जाएँ तो ध्यान से देखियेगा।

---

अब वो चित्र जिसे देखकर मैंने इस अनुपात के बारे में  पढ़ना चालु किया था। ये चित्र वैसे तो इन्टरनेट से लिया गया है  लेकिन पहली बार इसे मैंने 'Numerical methods for Engineers' किताब में देखा था... जिसमें एक छोटे से परिचय के साथ यही चित्र दिया गया है. अथेन्स के एक्रोपोलिस का... ईशा पूर्व पांचवी सदी में निर्मित ऐसे कई ग्रीक भवनों में यह अनुपात था... जिनमें सबसे प्रसिद्द पर्थेनोन नमक यह मन्दिर है। खँडहर का रूप ले चुके इस ईमारत की हुबहू कॉपी अमेरिका के टेनिसी प्रान्त की राजधानी नैशविले में बनाई गई है।

---

जाते-जाते उक़बा की मस्जिद को देख लीजिये... इसके मुख्य भवन और मीनारों में यह अनुपात आसानी से मिलता है... इसके अलावा आधुनिक समय में टोरंटो का सीएन टावर और  संयुक्त राष्ट्र के मुख्य भवन में यह अनुपात है। वैसे ये तो कुछ प्रसिद्द उदहारण हैं... इनके अलावा ऐसे कितने ही भवन होंगे जिनमे यह अनुपात ढूंढा जा सकता है. अपने ताजमहल में भी इसकी उपस्थिति कुछ शोधकर्ताओं ने ढूंढ़ निकाली है !

 

अगली पोस्ट में प्रकृति से कुछ उदहारण देखते हैं... डीएनए से लेकर गैलेक्सी तक में इस दैविक अनुपात की उपस्थिति... !

---

इस श्रृंखला के शुरुआत से ही आप सब का सहयोग और उत्साहवर्धन मिलता रहा है... मसिजीवीजी ने पिछले दिनों जनसत्ता के अपने नियमित कालम में सुनहरा अनुपात और इस ब्लॉग कि चर्चा की.  लवली कुमारी ने भी बड़े अच्छे सुझाव भेजें हैं. आप सबका आभार. आशा है ऐसे ही मार्गदर्शन मिलता रहेगा... और साथ बना रहेगा.

---

~Abhishek Ojha~

सुनहरा अनुपात और चित्रकारी

चित्रकारी की बात हो तो दिमाग में विन्ची का नाम शायद सबसे पहले दो-तीन नामों में से आ जाय और अगर मोनालिसा का नाम इसमें सबसे पहले आए तो कोई आश्चर्य नहीं होना चाहिए। विन्ची की कलाकृतियों में तो हजारों चीज़ें ढूंढ़ ली जाती हैं तो फिर सुनहरा अनुपात ढूँढना कौन सी बड़ी बात है। वर्चुवियन मैन में इस अनुपात की उपस्थिति तो हम देख ही चुके हैं... आज कुछ और चित्रों पर गौर करें: (भला हो इन्टरनेट का सारे चित्र सर्च किए हुए हैं)।

अब अगर लियोनार्दो दा विन्ची के सहयोगी लुका पसिओली (Luca Pacioli)

ने अगर कह दिया 'बिना गणित के कोई कला नहीं' तो क्या ग़लत कहा ! लियोनार्दो के अलावा भी हजारों पेंटिंग में ये अनुपात देखने को मिलता है। अब ये पेंटिंग देखिये कैसे फिट बैठ जाती है सुनहरे आयत में. विन्ची की 'लास्ट सपर' तो आपने सुनी ही होगी... इसके तो छोटे-छोटे हिस्से को मैग्निफाई करके देखने पर भी ये अनुपात मिल जाता है। पूरे चित्र का वर्गीकरण ही देख लीजिये।

शरीर के विभिन्न हिस्सों के अनुपात के रूम में देखा जाना भी शायद एक कारण रहा की चित्रकारों ने इसी अनुपात में पेंटिंग के चरित्रों की बनाया। अब माइकल एंजेलो की प्रसिद्द मूर्ति डेविड को देख लेते हैं: कमाल की बात ये है की डेविड के ये अनुपात विन्ची के वर्चुवियन मैन से एकदम मिलते हैं। वर्चुवियन मैन और आदर्श मानव चेहरे आप पिछली एक पोस्ट में यहाँ देख सकते हैं।

अब नए जमाने में एंड्र्यू रोजेर्स की ये कलाकृति भी देख लीजिये इसका नाम ही 'सुनहरा अनुपात' है, पत्थर और सोने से बनी ये कलाकृति जेरुसलम में स्थित है जो फिबोनाच्ची क्रम पर आधारित है। (एंड्र्यू रोजर्स बड़ी रोचक कलाकृतियाँ बनाते रहे हैं, आप उनके लिंक पर जाकर देख सकते हैं।)
अगले पोस्ट में कुछ स्थापत्य कला के नमूने देखते हैं... अब स्थापत्य कला हो और सुनहरा अनुपात तो पिरामिड भी आना ही चाहिए !

~Abhishek Ojha~

सुनहरा आयत, अनुपात और फिबोनाच्ची (बातें गणित की भाग... XV)

पिछली पोस्ट से उस सुनहरी दास्ताँ को आगे बढाते हैं. हमने सुनहरे अनुपात (Golden Ratio) की परिभाषा तो जान ही ली थी. आज वाली पोस्ट में थोडी गणित है (बस जोड़-घटाव) पर इसके बाद आने वाली ३-४ पोस्ट में एक भी अंक नहीं आएगा.

फिबोनाच्ची क्रम अंकों का एक क्रम होता है. जिसकी पहली और दूसरी संख्या १ होती है. उसके बाद हर अगली संख्या पिछली दो को जोड़ने से मिलती है, अर्थात फिबोनाच्ची क्रम ऐसा होता है: १, १, २, ३, ५, ८, १३, २१,.... आप देख सकते हैं क्रम के अंक पिछले दो अंकों के जोड़ने से बने है. ये हो गया फिबोनाच्ची क्रम (इस क्रम की संख्याओं को फिबोनाच्ची संख्या के नाम से जाना जाता है)...

अब एक काम करते हैं इस क्रम के हर अंक में उसके पिछले वाले अंक से भाग दे देते हैं। तो नया क्रम कुछ ऐसा होगा:

१, १/१, २/१, ३/२, ५/३, ८/५, १३/८, २१/१३, ...

अब अगर कैलकुलेटर उठा के देखें तो ये संख्याएं कुछ ऐसी आएँगी:

१, १, २, १.५, १.६६, १.६, १.६२५, १.६१५,...

अगर ये काम और बड़े अंकों के लिए करें तो यह धीरे-धीरे सुनहरे अनुपात की तरफ़ पहुच जाता है (१.६१८...). ये एक और तरीका है दैविक अनुपात तक पहुचने का... रास्ते अलग हो सकते हैं पर सत्य तो एक ही है ! जितने बड़े फिबोनाच्ची अंक लीजिये उतना सही सुनहरा अनुपात मिलेगा। अनंत के जितना करीब, सत्य के उतना ही पास !

आगे बढ़ने से पहले एक बात: वो हर चीज़ जिसमें सुनहरा अनुपात या आयत होता है मनुष्य को अच्छी लगती है चाहे वो कोई पेंटिंग हो या किसी का चेहरा, या फिर कोई वस्तु... सुनहरा अनुपात और सुन्दरता की चर्चा किसी और पोस्ट में !

अब आयत (Rectangle) की बात (वो छैंया-छैंया में 'आयत की तरह मिल जाए कहीं' से थोड़ा अलग है)। ऐसा आयत जिसकी भुजाओं का अनुपात 'सुनहरा अनुपात' हो उसे सुनहरा आयत कहते हैं। मतलब ये की आयत की लम्बाई को चौडाई से भाग देने पर १.६१८.... आए। इसकी कई खासियत में से एक ये भी है की अगर इसमें से एक वर्ग काटकर अलग कर दिया जाय तो जो बचता है वो भी सुनहरा आयत ही होता है। जब इस पर पहली किताब आई और इसके गुण चित्रकारों को पता चले तो इसकी सुन्दरता का खूब इस्तेमाल किया गया। कई प्रसिद्द पेंटिंग्स में। बस इस कदर लोग मोहित थे कि इसे ऐसा अनुपात माना जाता है जिससे प्रकृति काम करती है... ये हुआ आयत और इसी से जुड़ी हुई एक रचना आगे बनाएं तो घुमावदार स्पायरल का चित्र बनता है. ये चित्र में एक आयत और दूसरा स्पायरल दोनों सुनहरे ! एक को सुनहरा आयत कहते हैं और दुसरे को सुनहरा स्पायरल.





अब प्रकृति में ये रचना आपको कहाँ-कहाँ दिखती है? कई जगह... जैसे कुछ तो इनमें ही देख लीजिये। गणित ने कैसे कुछ बहुत बड़ी-बड़ी कलाकृतियों और इमारतों को प्रभावित किया है... इसकी चर्चा अगली पोस्ट में करते हैं।

---

पिछले पोस्ट पर आई द्विवेदीजी और मसिजीवीजी की टिपण्णी और उनके जवाब भी देखने लायक हैं. ये मत कह दीजियेगा की यही क्या कम था जो जाते-जाते और लिंक ठेले जा रहे हो :-)

---

~Abhishek Ojha~

कलाकारों और वास्तुशिल्पियों की पसंद: सुनहरा अनुपात (बातें गणित की भाग... XII)

चिटठा चर्चा में पढ़ा कि बिना पोस्ट्स के ब्लॉग ठूंठ हो जाते हैं तो ध्यान आया कि अब इस ब्लॉग को तो ठूंठ ही कहेंगे। गर्मी की छुट्टी भी एक महीने की ही होती है तो सोचा की कुछ ठेल ही दिया जाय अब बहुत हो गया। तो लीजिये प्राचीन से आधुनिक समय तक चित्रकारी से लेकर स्थापत्य तक में उपयोग होने वाले इस सुनहरे अनुपात के बारे में जान लेते हैं।

अनुपात (रेशियो) तो आप जानते ही होंगे, 'वही एक बट्टा दो... दो बट्टे चार, छोटी-छोटी बातों में बँट गया संसार'। एक संख्या को दुसरे से भाग दे दीजिये और वो हो जाता है एक अनुपात। तो ऐसे अनंत अनुपात हो सकते हैं... वैसे ही जैसे अनंत अंक होते हैं। अब इस अनंत अनुपातों में से ये अद्वितीय अनुपात है... जिसे सुनहरा अनुपात (गोल्डन रेशियो) कहते हैं। इसकी खासियत क्या है? अरे भई खासियत ही खासियत है... एक पोस्ट में तो नहीं आ पायेगी। पहले ये जान लेते हैं की ये होता क्या है... ना भी समझ में आए तो कोई बात नहीं है, कम से कम ये तो जान ही सकते हैं की दुनिया की सबसे मशहूर चित्रकार की पेंटिंग और कुछ मशहूर प्राचीन भवनों में इसका उपयोग हुआ था।

कोई भी दो भिन्न संख्या ले लीजिये, अब दो है तो एक बड़ा एक छोटा होगा ही, यदि दोनों के योग को बड़ी संख्या से भाग देने पर वही अनुपात आए जो बड़ी को छोटी से भाग देने पर. तो इस अनुपात को सुनहरा अनुपात कहते हैं (इसे दैविक अनुपात भी कहते हैं). गणितज्ञों को ये रोचक लगा तो वहीँ कलाकारों को इसमें खूबसूरती दिखी। अगर इसे हल किया जाय तो इस अनुपात का मान १.६१८ के लगभग होता है। पाई की तरह ही दशमलव के कई अंको तक इसे निकाला जा सकता है. इस एक अनुपात पर केवल गणितज्ञ ही नहीं कई विधाओं के लोगों ने सालों तक काम किया है... इसका इतिहास करीब २५०० साल पुराना है। इस अकेली संख्या पर कई किताबें है. जी हाँ एक संख्या पर कई किताबें. इस अनुपात का पहला लिखित विवरण युक्लिड द्बारा लिखा गया पर उससे पहले भी इसकी उपस्थिति यूनानी मूर्तियों में देखने को मिलाती है। यूनानियों ने पहली बार ज्यामितीय रचनाओं में इसकी उपस्थिति पर गौर किया. पर सबसे ज्यादा उपयोग हुआ पुनर्जागरण के समय पर जब इसकी खूबसूरती पर कुछ लोगों ने लिखा और फिर चित्रकार, मूर्तिकार, दार्शनिक सबने उपयोग किया।

इस संख्या के गणितीय गुण तो मैं लिखने से रहा क्योंकि इस ब्लॉग पर गणित नहीं लिखा जाता :-) तो इसके उपयोग के कुछ उदहारण देखते हैं। सबसे पहले मशहूर चित्रकार लिओनार्दो दा विन्ची की पेंटिंग देखते हैं। बाबा लिओनार्दो भी कमाल के आदमी थे... सब कुछ करते थे। चित्रकार, मूर्तिकार, गणितज्ञ, अभियंता, लेखक, संगीतज्ञ और पता नहीं क्या-क्या कभी उनकी एक किताब उठा के देखिये क्या डिजाईन बनायी थी उस ज़माने में उन्होंने ! ढूंढने वालों ने उनकी कुछ ५० से ज्यादा पेंटिंग्स में इस अनुपात को ढूंढ़ निकाला. इनकी मशहूर पेंटिंग 'वर्चुवियन मैन' की एक व्याख्या देखिये... और मोनालिसा में भी ये अनुपात ढूंढ़ ही लिया गया, मोनालिसा जैसी पेंटिंग बिना गणित के बन जाय... ऐसा कैसे हो सकता है !




स्थापत्य कला में इसका उपयोग देखना हो तो तकरीबन ४५० वर्ष ईशा पूर्व अथेन्स का एक्रोपोलिस है। इसमें यह अनुपात दिखा क्या आपको? थोड़ा मुश्किल है, मुझे भी नहीं दिख रहा।


वैसे अब इस संख्या की चर्चा हो ही गई है तो इन सब पर एक-एक मजेदार पोस्ट बन जायेगी। तो विस्तृत जानकारी अगले कुछ पोस्ट में आती रहेगी. इन सब के अलावा ये संख्या जीव विज्ञान और संगीत में भी आती है... उफ्फ़ ! संगीत और गणित? यही बाकी रह गया था। पर आपमें से बहुत संगीत में रूचि रखते हैं तो शायद आपको ये अच्छा लगे कि कैसे एक संख्या संगीत में उपयोग हो सकती है... आख़िर दैविक संख्या है !

अब आपको एक और गुण बता दूँ. ये अनुपात होता है १.६१८... अब जरा कैलकुलेटर उठा के १/१.६१८ निकालिए ये भी .६१८... आता है।

बहुत सारे गुण है जब कई किताबें हैं तो एक पोस्ट में क्या होगा। पर आज ब्लॉग को ठूंठ होने से बचाने के लिए इतना ही। आने वाली कुछ पोस्ट इस दैविक संख्या पर। देखते हैं कहाँ-कहाँ मिलता है। निराशा तो नहीं मिलेगी हाँ ये हो सकता है की आप भी इस सुनहरे अंक की उपस्थिति अपने शरीर के साथ-साथ आस-पास की कई चीज़ों में देखने लगें !

~Abhishek Ojha~


सारे चित्र विकिपीडिया से।

एक महिला गणितज्ञ के गणित प्रेम की दुखद कहानी ! (बातें गणित की... भाग XI)

प्रेम और दुःख का गहरा नाता है. जहाँ एक आ जाय दूसरा आ ही जाता है. और इस प्रेम में भी दुःख आया... महिला होने का अभिशाप भी. आप क्या सोच रहे हैं की जरूर भारत की कहानी होगी ! लेकिन ऐसा नहीं है... ये बात है फ्रांस की.

सोफी जर्मैन फ्रांस की एक महिला गणितज्ञ थी. पर दुर्भाग्य से उनका जन्म तब हुआ था (सत्रहवी शताब्दी) जब महिलाओं को यूरोप में समान अधिकार नहीं थे. बाकी सब तो ठीक लेकिन गणित पढ़ना औरतों के लिए खासकर बुरा माना जाता था. इसे पुरुषों का काम समझा जाता था. शायद यही कारण है की महिला गणितज्ञों की इतनी कमी रही है इतिहास में.

सोफी का जन्म एक अच्छे घराने में हुआ था और बचपन में वो अपने पिता के पुस्तकालय में बैठ कर पढा करती. इसी दौरान उन्हें एक किस्सा पढने को मिला. कहते हैं की आर्कीमिडिज (Archimedes) को एक सिपाही ने उस समय मार दिया जब वो ज्यामिति की कुछ संरचनाओं में लीन थे और उन्होंने सिपाही के सवालों का उत्तर देने की जरुरत नहीं समझी. शहर पर हमला हुआ था और वो गणित में लीन थे. इस किस्से से सोफी सोच में पड़ गई की जब कोई इस विषय में इस तरह तल्लीन हो सकता है तो जरूर इसमें कोई बात होगी. और उन्होंने गणित पढ़ना चालु किया. पर समस्या तब आई जब परिवार वालों को पता चला, परिवार वालों की पूरी कोशिश रही की ये गणित न पढ़े. तब के जमाने में यूरोप में ये काम लड़कियों के लिए बिल्कुल उपयुक्त नहीं समझा जाता था. तब लड़कियों को विश्वविद्यालयों में भी प्रवेश नहीं दिया जाता था. ख़ुद से पढ़ के भी क्या करती?

उनका गणित से प्रेम का ये आलम था की सोफी छुप कर घर के ऐसी जगहों पर गणित पढ़ा करती जहाँ कोई नहीं जाता. मोमबत्ती जला कर... फ्रांस में पड़ने वाली कड़ाके की ठंढ में भी वो जब घर के लोग सो जाते तो गणित पढ़ा करती. अपने प्यार के लिए तकलीफ सहती रही. घर वालों ने बाद में हार मान ली और परेशान करना छोड़ दिया. पर ये प्यार उन्हें इतनी आसानी से नहीं मिलने वाला था. गणित ख़ुद से पढ़ती तो ये कुछ पता नहीं होता की जो कर रही हैं सही है या ग़लत. ये भी नहीं पता होता था की जिन चीज़ों पर काम कर रही है कहीं वो पहले ही तो नहीं खोज लिए गए! ठीक उसी तरह जैसे रामानुजन, हार्डी से मिलने के पहले किया करते थे. कितना ही गणित वो ख़ुद लिख गए जिसकी खोज उस समय तक की जा चुकी थी. (रामानुजन की कहानी की तो श्रृंखला बन ही जायेगी, अभी उन पर एक और किताब पढ़ रहा हूँ. वो भी ख़त्म हो जाय तो लिखता हूँ). बिना औपचारिक शिक्षा के उन्हें कुछ पता ही नहीं था.

पर जहाँ चाह वहाँ राह ! उन्होंने एक नया तरीका निकाला... सेक्सपियर के ट्वेलव्थ नाईट की तरह उन्होंने एक ऐसे लड़के का छद्म नाम ले लिया जो पढ़ाई छोड़ चुका था, और वो उसके नाम से प्रश्न पत्रों का हल जमा कर देती. महान गणितज्ञ लैग्रंजे (Lagrange) ने जब उत्तरों को देखा तो उन्होंने सोफी को मिलने बुला भेजा और सोफी को अपना राज खोलना पडा. लैग्रंजे ने सोफी की तारीफ तो की पर फिर भी नियम के हिसाब से वो विश्वविद्यालय में प्रवेश नहीं ले सकती थी. इसी बीच सोफी एक और महान गणितज्ञ गॉस (Gauss) को अपने काम भेजती और गॉस पत्रों में जवाब दिया करते. यहाँ भी वो अपने छद्म नाम का ही इस्तेमाल करती. इस तरह कुछ दिनों तक चला पर ये बात भी ज्यादा दिनों तक नहीं चली. नेपोलियन ने गॉस के शहर प्रसिया (Prussia) पर हमला किया तो सोफी को बचपन वाली कहानी याद आ गई और उन्हें लगा कि कहीं आर्कीमिडिज वाली घटना गॉस के साथ भी न हो जाय. इसलिए उन्होंने अपनी एक सहेली को गॉस का ख़ास ध्यान रखने को कहा, उस सहेली ने गॉस को सब कुछ बता दिया. गॉस को बहुत आश्चर्य हुआ... की एक महिला भी गणित पर इतना अच्छा काम कर सकती है ! और उन्होंने सोफी को जो पत्र लिखा उसमें उनकी खूब प्रशंसा की. पर इस घटना के चंद दिनों बाद ही गॉस गोटिन्गेन विश्विद्यालय में खगोल शास्त्र के प्रोफेसर बन गए और गणित पर काम करना कम कर दिया और इसके साथ ही पत्र व्यवहार भी बंद हो गया.

पर समय के साथ सोफी का गणित प्रेम और संघर्ष जारी रहा... वो फ्रेंच गणित अकादमी में अपने काम को भेजती तो... काम उच्च कोटि का होते हुए भी उसमें कई छोटी-छोटी गलतियाँ होती. ऐसा अक्सर गणित में होता है पर अगर साथ में काम करने वाले होते हैं तो चर्चा और सुझाव से ये गलतियाँ हटाई जाती हैं. पर उन्हें मदद करने वाला कोई न था. फिर भी अंततः एक ऐसा समय आया जब वो अकादमी की बैठक में जाने वाली पहली ऐसी महिला बनीं जो किसी गणितज्ञ की पत्नी नहीं थी. इन सबके साथ गॉस ने उन्हें मानद डिग्री देने की सिफारिस भी की... उन्हें ये दी जाने वाली थी पर उसके पहले ही वो दुनिया छोड़ चली.

आज वो पहली महिला गणितज्ञ के रूप में जानी जाती हैं जिसने अच्छे और उपयोगी प्रमेयों की खोज की. सोफी लिखित कुछ दस्तावेजों से ये भी बात सामने आई की फ़र्मैट के प्रमेय पर उनकी सोच सही दिशा में थी. जहाँ उस समय के सारे गणितज्ञ किसी एक ख़ास अंक के लिए प्रमेय को साबित करने की कोशिश करते वहीँ सोफी ने एक विस्तृत सोच से शुरुआत की और कई सारे सिद्धांतों की मदद से पूरा प्रमेय एक साथ हल करने की कोशिश की. पर दुर्भाग्य न औपचारिक शिक्षा मिल पायी ना ही किसी गणितज्ञ का सहयोग... इतिहास के पन्नों में ऐसी कितनी ही प्रतिभाएं दफ़न हो गयीं... कारण बस यही था की वो महिला थी. नहीं तो आज उनका नाम कहीं और होता.... और पहली महिला गणितज्ञ होने के खिताब के साथ-साथ मुख्य धारा के महान गणितज्ञों में भी उनकी गिनती होती.

~Abhishek Ojha~

चित्र साभार: http://www.agnesscott.edu/lriddle/women/germain.htm

एंड्र्यू वाइल्स, फील्ड्स मेडल और एक महिला गणितज्ञ (बातें गणित की... भाग X)

पिछले पोस्ट में हमने देखा की किस तरह एंड्र्यू वाइल्स ने सात सालों की कठिन मेहनत के बाद एक बड़ा सा हल निकाला. ये उस सवाल का हल था जिसे हल करने की कोशिश अब तक के सबसे महान गणितज्ञ कर चुके थे. एंड्र्यू वाइल्स ने कितनी मेहनत की थी इसका अंदाजा तो आप पिछले पोस्ट पर उनकी तस्वीर देखकर ही लगा सकते हैं. एंड्र्यू वाइल्स ने गणित का महानतम सवाल हल किया और एक सवाल के हल ने उन्हें महान गणितज्ञों की श्रेणी में ला खड़ा किया. पर गॉस, ओय्लर जैसे गणितज्ञ क्या इनसे कमजोर थे? ऐसे सवाल तो उठने ही नहीं चाहिए पर लोग उठाते हैं. और मेरे जैसे जो गॉस की विद्वता के घोर प्रसंशक हैं वो यही कहते हैं कि न तो गॉस ने सात साल तक इस सवाल पर काम किया और ना ही तब गणित इतना विकसित था. हाँ ये बात और है की अगर गॉस ने ७ सालों तक इस सवाल पर काम कर दिया होता तो आज नंबर थियोरी की कई शाखाएं होती. गॉस की विद्वता तो आगे कई पोस्ट में आएगी ही. पर एंड्र्यू वाइल्स की विद्वता भी अतुलनीय है और ऐसे विवाद सही में कोई मायने नहीं रखते. एंड्र्यू वाइल्स अपने गणित के अनुभव के बारे में कहते हैं:

अगर मुझे गणित पर अपने अनुभव के वर्णन करने को कहा जाय तो शायद मैं कहूं की यह एक अंधेरे कमरे में प्रवेश करने की तरह है, पहला कमरा... अंधकारमय, बिल्कुल अंधकारमय. इधर-उधर भटकना, उछलना और फिर धीरे-धीरे पता चलने लगता है की कहाँ कौन सा फर्नीचर है. और फिर अंततः ६ महीने या ऐसे ही कुछ समय पश्चात पता चलता है की स्विच किधर है, उसे दबा देना और फिर सबकुछ जगमगा उठता है... तब सब कुछ दिखने लगता है और ये पता चलता है कि मैं कहाँ हूँ ! -- एंड्र्यू वाइल्स बीबीसी की एक डॉक्युमेंट्री के प्रारम्भ में.

हर चार साल पर दिया जाने वाला फील्ड्स मेडल गणित के क्षेत्र का नोबेल पुरस्कार कहा जाता है. तो फिर एंड्र्यू वाइल्स को निर्विवाद रूप से मिल जाना चाहिए. पर फील्ड्स मेडल में एक शर्त होती है की पुरस्कार मिलने वाले साल तक गणितज्ञ की आयु ४० से ज्यादा नहीं होनी चाहिए ! एंड्र्यू वाइल्स का जन्म १९५३ में हुआ था और उस हिसाब से १९९४ में वो एक साल ज्यादा के हो गए थे. नियम तो फिर नियम ही है तो उन्हें ये पुरस्कार नहीं दिया गया*. पर फील्ड्स मेडल की समिति ने उन्हें पुरस्कृत करना ही उचित समझा और १९९८ में उन्हें अलग से एक विशेष रजत-फलक दिया गया. फील्ड्स मेडल पर महान गणितज्ञ आर्कीमिडिस की तस्वीर होती है. ४० साल से कम क्यों? इसकी एक आम धारणा ये है की गणितज्ञ अपनी मौलिक सोच (Original ideas) ४० के पहले ही सोचते हैं इसके बाद वो गणित पर बस काम करते हैं खोज तो कम उम्र में ही होती है. इस चालीस साल की बात से याद आया जी एच हार्डी की ये बात जो उन्होंने अपनी पुस्तक 'A Mathematician's Apology' में लिखी है.**

"किसी भी गणितज्ञ को ये नहीं भूलना चाहिए की गणित युवा लोगों का खेल है. इसका सबसे आसान उदहारण यही है की रोयल सोसाइटी में गणितज्ञों की औसत उम्र सबसे कम है. और भी कई उदहारण लिए जा सकते हैं न्यूटन ने ५० की उम्र में गणित छोड़ दिया. वे मानते थे की ४० वर्ष की उम्र के साथ ही उनकी मौलिक रचनात्मकता के महानतम दिन ख़त्म हो गए...
...गैल्वास की मृत्यु २१ साल की उम्र में हो गई. रामानुजन ३३ में और रीमान ४० की उम्र में चल बसे. कुछ लोगों ने इस उम्र के बाद भी काम किया है जैसे की गॉस ने डिफेरेंसिअल जियोमेट्री तब लिखी जब वो ५० साल के थे, लेकिन इसका विचार उन्हें १० साल पहले ही आ गया था. मेरी नज़र में कोई बड़ी गणितीय खोज ४० की उम्र के बाद किसी ने नहीं की. और अगर किसी की इस उम्र के बाद गणित गणित में रूचि कम हो जाती है तो इससे न तो उसकी न गणित की ही कोई क्षति होने वाली है." --जी एच हार्डी

कई गणितज्ञों ने फ़र्मैट के अन्तिम प्रमेय पर काम किया ये तो हम देख ही चुके है पर अगर इस महिला गणितज्ञ की चर्चा न हो तो शायद श्रृंखला अधूरी रह जाय. पोस्ट लम्बी हो रही है इसलिए आगे नहीं लिखूंगा बस इतना बताता चलूँ की इस महान गणितज्ञ को महिला होने का खामियाजा भुगतना पड़ा. नहीं तो आज इतिहास में कहीं और ज्यादा नाम होता... फ़र्मैट के अन्तिम प्रमेय पर सही तरीके से सोचने वाले बहुत कम लोगों में वो एक थी. उस संघर्ष, दुःख और गणित से प्यार की कहानी अगले पोस्ट में.

---

चित्र: साभार, विकिपीडिया
*ऐसे पुरस्कारों के साथ ऐसी कहानियाँ तो होती ही है... शायद नोबेल पुरस्कार की सबसे बड़ी कमी हमेशा के लिए ये रह जाय की गांधीजी को नोबेल पुरस्कार नहीं मिला. गांधीजी ऐसे किसी पुरस्कार के मोहताज तो न थे... पर ये मलाल शायद नोबेल समिति को रहे. इस बारे में अगर रूचि हो तो नोबेल पुरस्कार की आधिकारिक वेबसाइट पर इस लिंक पर पढ़ आए.
**पुस्तक की सॉफ्ट कॉपी पास में होने का यह एक बहुत बड़ा फायदा है... जब जिस पैराग्राफ की जरुरत हो खोल के सर्च कर लो.

सात साल में बना १००० पन्नों का हल (बातें गणित की... भाग IX)

पिछले पोस्ट में हमने देखा की किस तरह अनसुलझे सवालों का पिटारा तैयार हो गया और सारे अनसुलझे सवाल एक-दुसरे से जुड़े हुए थे. इस बीच विशेषज्ञों ने सलाह दी की पानी सर के ऊपर से जा रहा है और बेहतर होगा की अब नंबर थियोरी से ऊपर उठकर सोचा जाय. और लोग नए जोश से इस सवाल को हल करने में लग गए. अब एक और गणितज्ञ का परिचय हो जाय. एंड्र्यू वाइल्स (Andrew Wiles) कैम्ब्रिज विश्वविद्यालय से गणित पढ़कर प्रिन्सटन पहुच गए पढाने, अभी भी वहीँ पढाते हैं...

इस दौरान एक सवाल हल हो गया. बर्कली स्थित कैलिफोर्निया विश्वविद्यालय के केन रिबेट (Ken Ribet) ने जीन पिएरे के एप्सिलोन अनुभाग (Epsilon Conjecture) को साबित कर दिया. ये ख़बर सुनकर एंड्र्यू वाइल्स ने तानिमाया अनुभाग हल करने की ठान ली... क्योंकि अगर ये हो गया तो फिर फ़र्मैट का अन्तिम प्रमेय भी हो गया. और फिर सात सालों तक सारे शोध कार्य छोड़कर एकांत में... वो काम करते रहे... केवल एक सवाल पर... गणित के महानतम सवाल पर. कुछ रिसर्च पेपर से, पर ज्यादातर ख़ुद के दिमाग से... वो काम करते रहे. कहते हैं की २ साल तक वो सवाल में अपने आपको डुबाये रहे ताकि एक स्ट्रेटजी सोच सकें.

तानियामा के अनुसार इलिप्टिक कर्व और मोडुलर फोर्म्स दोनों सेट एक ही हैं... यानी हर एक सदस्य के लिए दुसरे में वैसा ही सदस्य मौजूद है... पर समस्या ये की दोनों सेट में अनंत सदस्य ! गिनें तो कैसे गिनें? उन्होंने सहायता ली गैल्वास (Galois) के सिद्धांतों की. (गैल्वास की मजेदार के साथ-साथ दुखद कहानी जल्दी ही किसी पोस्ट में). गैल्वास के सिद्धांत ने कमाल किया और अब समस्या रह गई गैल्वास के सिद्धांत से मोडुलर फॉर्म के तुलना की. तीन साल में इतना हो पाया और ये बात कोई नहीं जानता था सिवाय एंड्र्यू की पत्नी के! इसके बाद कई सारे शोध और कईयों की थियोरी का इस्तेमाल किया एंड्र्यू ने. वो ये बातें किसी को नहीं बताते दो कारण थे एक ये की वो अपना ध्यान नहीं भंग करना चाहते थे और दूसरा ये... कौन कहे की आज के जमाने में भी लोग फ़र्मैट के अन्तिम प्रमेय पर काम करते हैं :-) वो ये बातें पत्नी के अलावा केवल अपने मित्र निक कट्ज़ (Nick Katz) को बताते थे.

और फिर १९९३ में न्यूटन इंस्टीच्युट ऑफ़ मैथेमेटिकल साइंसेस, कैम्ब्रिज में अपने गाइड द्बारा आयोजित कांफ्रेंस में उन्होंने व्याख्यान दिया 'इलिप्टिक कर्व, मोडुलर फॉर्म और गैल्वास रेप्रेसेंटेशन' पर. व्याख्यान में कई नए विचार प्रस्तुत किए गए पर न तो व्याख्यान के शीर्षक में न ही व्याख्यान में फ़र्मैट की चर्चा थी. जब व्याख्यान देते-देते वो अंत तक पहुचे तो सुनाने वालों के चहरे गंभीर हो गए थे... सबको लग गया था की अब कुछ बड़ा होने वाला है और फिर उन्होंने लिख दिया 'फ़र्मैट के अन्तिम प्रमेय का कथन' और लिख दिया हेंस प्रूव्ड !

और अगले दिन हर अखबार में ये ख़बर आई की अंततः प्रमेय सिद्ध हो गया !

एक कमिटी बनी लंबे चौडे हल की जांच के लिए और फिर निकली एक गलती... [गणित के प्रूफ़ में गलती होना तो आम बात है... उनकी तो हो गई. हम तो जान बुझ के कर दिया करते थे... जब प्रूफ़ नहीं आ रहा हो तो एक तरफ़ से बढ़ते-बढ़ते कहीं तक गए, दूसरी तरफ से चले तो कहीं और. फिर बीच में एक लाइन ऐसी होती थी जहाँ दोनों को बराबर दिखा देते :-) पर आईआईटी के प्रोफेसर कभी नंबर नहीं दिए... उत्तर पुस्तिका में जब How? Why? और So What? How Come? जैसी टिपण्णी लिखी मिल जाती तो चुप-चाप उत्तर पुस्तिका को मोड़ के रख लेते :(] इधर फिर वापस एंड्र्यू को लगना पड़ा सवाल पर... पर इस बार मामला इतना आसान नहीं था, पहले वो बिना किसी को बताये इस सवाल पर शान्ति से काम करते पर अब सबकी नज़रें इस पर लगी हुई थी... (गनीमत है 'आज तक' जैसे चैनल न थे अमेरिका में तब, नहीं तो बेचारे कुछ ना कर पाते). ध्यान नहीं लग पा रहा था और पहली बार एंड्र्यू ने किसी की मदद ली और उन्होंने अपने पूर्व छात्र टेलर को बुला भेजा. एक साल तक कोई सफलता हाथ नहीं लगी... और फिर एक दिन, उन्हें समस्या दिख गई और उन्होंने उसे निपटा दिया. और फिर फ़र्मैट का अन्तिम प्रमेय पूरी तरह से हल हो गया.

पूरा हल १००० हजार पन्नो का हुआ... जो व्याख्यान 'न्यूटन इंस्टीच्युट ऑफ़ मैथेमेटिकल साइंसेस' में उन्होंने दिया था वही कुछ २०० पन्नो का था. तो फ़र्मैट ने अगर कहा था की किताब के हाशिये में कम जगह है तो क्या ग़लत कहा था ! पिछले पोस्ट की टिपण्णी में ज्ञानजी ने कहा की उनके उपनिदेशक ने इस सवाल को लेकर फील्ड्स मेडल के सपने दिखाए थे... तो क्या एंड्र्यू वाइल्स को फील्ड्स मैडल मिला? क्यों नहीं मिलेगा भाई, आख़िर उन्होंने गणित का महानतम सवाल हल किया था ! पर क्या और क्यों हुआ जानते हैं अगली पोस्ट में. (फील्ड्स मेडल गणित के क्षेत्र में नोबेल पुरस्कार के समान माना जाता है).

~Abhishek Ojha~

एक अनसुलझे सवाल से मिली मदद (बातें गणित की... भाग VIII)

पिछले पोस्ट में हमने चर्चा की थी फ़र्मैट के लिखे एक नोट से एक कठिनतम सवाल बन जाने की. हमने ये भी देखा की बड़े-बड़े गणितज्ञ धराशायी हो गए पर सवाल टस से मस नहीं हुआ.

पर इस बीच कुछ हुआ ही नहीं ऐसा भी नहीं है कई गणितज्ञों ने इस सवाल को कुछ ख़ास परिस्थितियों के लिए सही सिद्ध कर दिया... ओय्लर (Euler) ने n को ३ लेकर किया तो द्रिच्लेट (Dirichlet) और लिजेंद्रे (Legendre) ने मिलकर ५ के लिए. इसी तरह कुछ और अंको के लिए सिद्ध किया गया, १८५७ में क्युम्मर (Kummer) ने रूढ़ संख्याओं के एक ख़ास वर्ग के लिए सिद्ध किया. पर सारे अंको के लिए सिद्ध करना अभी भी दूर की बात थी. ब्रिटानिका एन्साइक्लोपेडिया में इस सवाल के जिक्र के अंत में लिखा गया था कि 'शायद यह प्रमेय कभी सही या ग़लत साबित न किया जा सके'.

महान गणितज्ञ हिल्बर्ट (Hilbert) से जब ये पूछा गया की वो इस सवाल पर काम क्यों नहीं कर रहे तो उन्होंने जवाब दिया कि 'इस सवाल के लिए मुझे तीन साल तक गहन अध्ययन करना पड़ेगा और उसके बाद भी संभवतः हार का सामना करना पड़े.' हिल्बर्ट और इस सवाल पर एक प्रसिद्द किस्सा भी है, उन दिनों जहाज का नया-नया आविष्कार हुआ था और हिल्बर्ट को एक कांफ्रेंस में जाना था उन्होंने कह दिया कि मैं 'फ़र्मैट के अन्तिम प्रमेय' पर बोलने वाला हूँ जब उनका प्रेजेंटेशन ख़त्म हो गया और फ़र्मैट का कोई जिक्र तक नहीं आया तब लोगों ने पूछा कि आप तो फ़र्मैट पर बोलने वाले थे. हिल्बर्ट ने जवाब दिया कि वो मैंने इसलिए कहा था कि अगर प्लेन क्रैश हो गया होता तो मैं भी फ़र्मैट कि तरह अमर हो जाता. लोगों को लगता कि मैंने सिद्ध कर लिया था.

इस बीच १९८८ में एक हल आया और खूब लोकप्रिय हुआ पर जब जांच हुई तो इसे ग़लत करार दिया गया... कुछ गणितज्ञों ने 'फ़र्मैट का अन्तिम प्रमेय कैसे साबित न करें' जैसे पेपर भी छपे जिसमें ये लिखा जाता कि इस तरीके से मैंने कोशिश कर ली है कोई फायदा नहीं !

सवाल कि कठिनता बढती गई और कहानियाँ भी बनती गई... इन सब के बीच १९५५ में २८ वर्षीय जापानी गणितज्ञ तानियामा (Taniyama) ने एक नया सवाल पेश किया... जो कहता है कि इलिप्टिक कर्व्स (Elliptic Curves) और मोडुलर फोर्म्स (Modular Forms) के बीच सम्बन्ध है... या फिर यूँ समझ लें कि छद्म वेश में दोनों एक दुसरे का ही रूप हैं. इसे समझने कि जरुरत नहीं बस इतना जान लीजिये कि ये नया सवाल कुछ ऐसा कहता था कि गणित की दो एकदम ही अलग चीजें एक-दुसरे से जुड़ी हुई है. लोगों को ज्यादा समझ नहीं आया, और इसी बीच १९५८ में तानियामा ने आत्म हत्या कर ली. उनके मित्र शमुरा (Shimura) ने इस सवाल पर और काम किया और लोगो तक इसे पहुचाया. अब कुछ फ़र्मैट की ही तरह तानियामा ने कह दिया था की ऐसा है... पर कोई प्रमाण इसका भी नहीं था. (इसे तानियामा-शिमुरा सवाल (Taniyama-Shimura Conjecture) के नाम से जाना जाता है).

पर क्या इस समानता के अलावा भी कोई और समानता थी? दोनों एकदम अलग... एक कहता है की इलिप्टिक कर्व और मोड्यूलर फॉर्म एक हैं... दूसरा कहता है की एक समीकरण का हल कोई ३ संख्याएं नहीं हो सकती ! दोनों में कोई सम्बन्ध नहीं... पर नए विचार ही तो कमाल करते हैं... १९८५ में ग्रेहार्ड फ़्रे नाम के जर्मन गणितज्ञ वो सोच दिखाया जो कभी कोई सोच ही नहीं सकता था. फ़्रे ने मान लिया की फ़र्मैट ग़लत हैं, यानी कम से कम एक हल होना चाहिए उनके समीकरण का ! पर ये मानकर उन्होंने ये पाया की अगर ऐसा हुआ तो एक ऐसी इलिप्टिक कर्व बन जायेगी जो मोडुलर नहीं होगी ! पर तानियामाजी कह गए थे की हर इलिप्टिक मोडुलर होनी चाहिए. बस उन्होंने एक और निष्कर्ष निकाल दिया की अगर फ़र्मैट ग़लत हैं तो फिर तानियामा भी सही नहीं हो सकते यानी उन्हें भी ग़लत होना पड़ेगा. इसी को तार्किक भाषा में लिख दें तो ये कथन ऐसा हो जाता है: अगर तानियामा का कथन सत्य है तो फ़र्मैट का अन्तिम प्रमेय भी सत्य होगा. तो अब ये दोनों अनसुलझे सवाल जुड़ गए. पर समस्या ये थी की फ़्रे चचा ने भी कुछ साबित नहीं किया, बस कमाल का विचार देकर उन्होंने सोचा की विशेषज्ञ लोग ये सब साबित कर देंगे. और ऐसा ही हुआ विशेषज्ञों ने काम करना चालु कर दिया (फ़्रे के विचार को जीन पिएरे के विस्तार के बाद एप्सिलोन अनुभाग के नाम से जाना गया).

अब देखिये सारांश...

- फ़र्मैट ने एक बात कही की ऐसा नहीं हो सकता.
- तानियामा ने कहा की दो बिल्कुल ही अलग गणितीय चीजें जो देखने में तो बिल्कुल अलग हैं लेकिन ध्यान से देखो तो एक ही है.
- फ़्रे और जीन पिएरे ने कहा की भाई अगर तानियामा सही हैं तो फ़र्मैट भी सही है.

अभी तक सबने बस कहा... किसी ने कुछ साबित नहीं किया. और गणित में अगर साबित करना हटा दिया जाय तो कोई फेल ही ना हो :-) बिना साबित किए कभी किसी बात का कोई मतलब है गणित में ... कुछ नहीं ! तो फिर इन अनसुलझे हुए सवालों की पोटली से आगे क्या हुआ? देख के तो यही लगता है की अनसुलझे सवालों का अम्बार लगता जा रहा है... बस सबके तार जुड़ रहे हैं... तो क्या ये तार कुछ सुलझा पायेगा? जानते हैं अगले पोस्ट में!

---

- समीरजी क्यों ये कह कर दुखी कर रहे हैं की मैं गणित जानता हूँ... गणित ही जान रहा होता तो कहानियाँ क्यों सुनाता :-) और आपके विकल्प अच्छे तो हैं पर फिजिबल नहीं ! फिजिबल विकल्पों का सेट लेकर आइये तो सुझाव मिलेगा.

- अनुराग जी धन्यवाद आपका... सप्ताह में एक से दो पोस्ट तक करने की कोशिश है... सम्भव हो पाया तो सारा श्रेय आपका.

---

~Abhishek Ojha~

गणित के महानतम सवाल का रोचक इतिहास (बातें गणित की... भाग VII)

आज चर्चा करते हैं गणित के महानतम सवाल की. सवाल इतना आसान की १० साल की उमर के बच्चे को समझ में आ जाय. और इतना कठिन की गॉस जैसे महानतम गणितज्ञ परेशान हो जाय. इस सवाल की कठिनता इसी बात से लगे जा सकती है की गॉस ने इस सवाल को हल करने की कोशिश की और अंत में परेशान होकर उन्होंने एक पत्र में लिखा था: "वास्तव में, मैं यह स्वीकार करता हूँ की मुझे इस सवाल में बहुत कम रूचि है और ऐसे तो कई सवाल बनाए जा सकते है, जिन्हें न तो सही साबित किया जा सकता है न ग़लत."

फ़र्मैट सोलहवी शताब्दी के एक महान गणितज्ञ थे, पेशे से वकील इस महान फ्रांसीसी गणितज्ञ ने गणित के कई क्षेत्रों में महतवपूर्ण योगदान किया. जब न्यूटन ने कलन (Calculus) का आविष्कार किया तो उन्होंने कहा की इसका विचार उन्हें फ़र्मैट के काम को देखकर ही आया. १६३७ में फ़र्मैट ने एक किताब पढ़ते हुए उस पर लिखा की "मेरे पास इस सवाल का एक अद्भुत हल है, लेकिन इस किताब के हाशिये पर इतनी कम जगह है की ये लिखा नहीं जा सकता." अब उस हाशिये की कम जगह ने ऐसा गुल खिलाया की ये सवाल गणित का कठिनतम सवाल बन गया. गॉस ने तो कोशिश की ही की उनके अलावा ओय्लर, गैल्वास जैसे गणितज्ञों ने भी हाथ आजमाया, ऐसा माना जाता है की इस बात के छपने के बाद कोई गणितज्ञ ऐसा नहीं रहा जिसने इसे हल करने की कोशिश न की हो. गणितज्ञ ही क्यों जो भी सुनता एक बार कोशिश कर लेता, है ही इतना सरल देखने में. और फ़र्मैट चाचा ने लिख ही दिया था की उनके पास हल है, सब सोचते की लगे हाथों नाम कमा लिया जाय. फ़र्मैट के नाम पर ही इसे 'फ़र्मैट का अन्तिम प्रमेय'(Fermat's Last Theorem) नाम से जाना जाता है.

सवाल कुछ इस तरह है: अगर n, २ से बड़ा हो तो x^n + y^n = z^n का कोई अशून्य हल नहीं हो सकता. अर्थात ऐसी कोई तीन शून्य से भिन्न संख्याएं (x,y,z) नहीं हो सकती जिसके लिए समीकरण सत्य हो. अगर आपने पाइथागोरस प्रमेय पढ़ा है तो यह n की जगह २ रखने पर होता है, n को अगर २ लें तो ऐसी कई संख्याएँ हैं जैसे x=3, y=4, z=5 (3^2 + 4^2 = 5^2). पर क्या n>२ के लिए ऐसी तीन संख्याएं x,y,z सम्भव हैं?

फ़र्मैट के साथ ही इसका हल भी चला गया और अब लोग इस बात पर लगे रहे की ये कथन सत्य है या नहीं. इस सवाल की खूबसूरती यही थी की सब कोई समझ जाता हर किसी को लगता की अरे इसमें क्या है हल किए देता हूँ ! पर सदियाँ बीत गई. इस सवाल ने कईयों के दिन और रातें ख़राब की. पाइथागोरस प्रमेय हल करना आसान था लेकिन २ से बढ़ते ही... फ़र्मैट ने कह दिया की संख्याएं सम्भव नहीं (और ये भी कह गए थे की उनके पास इस बात का प्रमाण भी है)... लेकिन ये बात साबित कैसे हो... ऐसी संख्याएं हो भी तो सकती है ! लोग साबित करने की कोशिश करते. कई ऐसे नंबर ही ढूंढ़ते जिसके लिए ये समीकरण सही हो जाय. वैसे तो फ़र्मैट ने किताबें पढ़ते हुए ऐसे कई नोट लिखे थे किताबों के हाशियों पर, सब साबित होते चले गए... अंत में बच गया ये और इसीलिए नाम पड़ गया 'फ़र्मैट का अन्तिम प्रमेय'.

अब कम्प्यूटर की खोज हो गई तो क्या ऐसा नहीं है की सारे नंबर के लिए चेक कर लो. ये कौन सी बड़ी बात है... लेकिन बड़ी बात है... क्योंकि ये काम कम्प्यूटर नहीं कर सकता! कितने नंबर आप चेक करेंगे?... हजारों, लाखों तब भी बहुत सारे बचे रहेंगे... आप अनंत तक कभी नहीं जा सकते... लाखों करोडो अंक कम करते जाएँ तब भी अनंत अंक बचे रहेंगे. ॐ पूर्णमदः पूर्णमिदं पूर्णात्पूर्णमुदच्यते पूर्णस्य पूर्णमादाय पूर्णमेवावशिष्य्ते॥

आप अनंत से अनंत निकाल ले तो भी अनंत ही शेष रहता है. तो कम्प्यूटर फ़ेल. यही कारण है की ऐसे प्रमाण को गणितज्ञ नकार देते हैं. गणित में कुछ भी साबित करने की प्रथा रही है. स्टेप-बाई-स्टेप ताकि कुछ गुन्जाईस ना बची रह जाय. गणितज्ञों को चुनौती बहुत पसंद है पर ये चुनौती उन्हें हराती रही. धीरे-धीरे ऐसा लगा की गणितज्ञों ने हार मान ली है... इस सवाल पर काम करना ना के बराबर हो गया. या यूँ कह लें की कोई भी इस पर काम करने से डरता था (जो करता भी छुप के करता, ताकि लोग हँसी ना उडाएं). तो फिर क्या हुआ इस सवाल का? क्या किसी ने हिम्मत की... अगर आप जानते तो अच्छी बात हैं, वैसे जानेंगे यहाँ पर बाकी कई सारी रोचक जानकारी के साथ अगले पोस्ट में !

इस सवाल पर कई किताबें है और एक प्रसिद्द डोक्युमेन्ट्री भी बनी. इस पोस्ट में कई बातें उस डॉक्युमेंट्री से भी ली जायेंगी.

कल रंजनाजी ने एक ब्लॉग समीक्षा लिखी इस श्रृंखला पर. आप इस लिंक पर जाकर पढ़ सकते हैं. बहुत-बहुत आभार रंजनाजी का. रंजनाजी ने कुछ ज्यादा ही बड़ाई कर दी है. पर उनका आशीर्वाद मिला है, खुश रहने का... तो खुशी-खुशी सर माथे पर.

---

- आंकडों वाली पोस्ट पर द्विवेदीजी की टिपण्णी से एक बात याद आई: हमारे समाजशास्त्र (Sociology) के एक प्रोफेसर सांख्यिकी(Statistics) के प्रोफेसर के पास आए थे और उन्होंने कहा की मेरे पास ये कुछ आंकडा है और मैं अपनी मान्यताओं को गणित का जामा पहनाना चाहता हूँ तो आप कोई ऐसा मॉडल बता दीजिये जिससे वो ही रिजल्ट आयें जो मेरी मान्यता का समर्थन करें.:-) तो गणित तो बेचारा गणित है उसका उपयोग भी लोग अपनी मर्जी से कर लेते हैं. मूक बेचारा क्या कर सकता है भला !
- समीरजी आपको वेटेड एवेरेज से डरने की जरुरत नहीं है... आप टिपण्णी करने वालो पर की जाने वाली हर तरह की अनाल्य्सिस में आउटलायर ही रहेंगे. किसी भी कर्व फिटिंग से पहले ही आप को बाहर कर दिया जायेगा :-) नहीं तो अकेले ही सारा कर्व स्क्यू कर देंगे आप.

---

चित्र साभार: विकिपीडिया

~Abhishek Ojha~

आंकडों की समस्या और ब्लॉगजगत का गणित (बातें गणित की भाग... VI)

पिछले पोस्ट पर आई दो टिपण्णीयाँ:

अनूप शुक्ल: अच्छा गणितीय उपयोग है। निष्कर्ष के लिये गणित सहयोगी है लेकिन ये आंकड़े जुटाना अपने में कठिन काम है।
masijeevi: रोचक काम करते रहे हैं आप।
कुछ और ब्‍यौरे रहते तो और अच्‍छा होता- ब्लॉगवाणी जैसी झलकियॉं हो गईं इस बात से हम भी सहमत हैं।
कुछ और मॉडलों पर विचार करें- कैसे तय हो कि आज की सबसे अच्‍छी पोस्‍ट किसकी होगी... कौन सी पोस्‍टें पढी जाएंगी किन पर टिप्‍पणी मिलेंगी और ऐसी कितनी होंगी जिनपर टिप्‍पणी तो मिलेंगी लेकिन पढ़ी नहीं जाएंगी... मतलब ब्‍लॉगजगत का गणित :))

अनूप जी ने बिल्कुल सही बात कही है, हमें तो आंकड़े दे दिए गए थे, लेकिन अगर ऐसे निष्कर्षों तक पहुचने में कुछ सबसे ज्यादा दिक्कत काम है तो वो है आंकडा इकठ्ठा करना. अपने देश में और मुश्किल, अपने देश में मुश्किल इसलिए की चीज़ें थोडी अव्यवस्थित हैं... या यूँ कहें की एकाउंटएबिलिटी नहीं है हर चीज़ की.अब देखिये जैसे पिछली पोस्ट में बनिए की दूकान से डिटर्जेंट का आंकडा इकठ्ठा किया गया था कनाडा में. उसमे किस परिवार ने क्या खरीदा?, महीने के किस तारीख को खरीदा?, उस घर में कितने लोग है? कितनी आय है? इस प्रकार से खूब आंकड़े थे. इन्हें इकठ्ठा करना वहां आसान था, हर ग्राहक को एक स्मार्ट कार्ड बाँट दिया गया और फिर काम आसान हो गया. वैसे ही अगर किस राज्य में कितनी गाडियां बिकी... किसी एक साल में ये जानना हो तो अपने देश में हर आरटीओ जाकर हर वर्ग में रजिस्टर हुई गाड़ियों की संख्या पता करो या फिर हर तरह के गाड़ी निर्माताओं से संपर्क करो. ये जानकारी हासिल करना उन देशों में आसान हो जाता है जहाँ सबकुछ कम्प्यूटर की सहायता से होता है. ये भी एक कारण है की रिसर्च पेपर उन देशों के आंकडों से ज्यादा छपते है और अपने यहाँ पूरी तरह से प्रभावी नहीं होते. अभी तक सांख्यिकी पर कुछ लिखा ही नहीं गया इस श्रृंखला में. तो आंकडो की समस्या की चर्चा उस पोस्ट के लिए छोड़ देते हैं।

आंकडों की समस्या बात उठ ही गई है तो आपको बताता चलूँ की वित्त और इनवेस्टमेंट बैंकिंग का एक मिनट भी आंकडों के बिना काम नहीं चल सकता. माइकल ब्लूमबर्ग सोलोमन ब्रदर्स नामक इनवेस्टमेंट बैंक में काम करते थे १९६६ से १९८१ तक. १५ वर्षों के अनुभव के बाद उन्हें आंकडों की समस्या हल करने की सूझी और उन्होंने १९८१ में ब्लूमबर्ग नाम की कंपनी खोली जिसका मुख्य काम हर तरह के आंकड़े और सुचना देना था. आज शायद ही कोई वित्तीय कम्पनी हो जो ब्लूमबर्ग के उत्पादों का इस्तेमाल ना करती हो. माइकल ब्लूमबर्ग अब दुनिया के सबसे अमीर आदमियों में से एक हैं फोर्ब्स के अनुसार उनकी संपत्ति ११.५ अरब अमेरिकी डालर के बराबर है. अभी न्यूयार्क शहर के मेयर हैं और दानी होने तथा मात्र १ डालर वार्षिक आय लेने के कारण जाने जाते हैं. ९/११ की घटना के बाद अपनी कर्मठता के लिए भी जाने जाते है, अमेरिकी चुनाव में राष्ट्रपति पड़ के उमीद्वार होने की भी अटकलें लगाई गई. तो आंकड़े कमाल कर सकते हैं, आपको कहाँ से कहाँ पंहुचा सकते हैं ये तो आपने देख ही लिया. ब्लूमबर्ग तथा रॉयटर्स का एक तरह से वित्तीय आंकडों के बाजार में एकाधिकार है. (चित्र में: माइकल ब्लूमबर्ग और एक ब्लूमबर्ग टर्मिनल) चित्र साभार: विकिपीडिया और http://blogs.pcworld.co.nz/pcworld/ck-live/bloomberg.jpg

अब बात ब्लॉग जगत के गणित की, मसीजीवीजी के सारे सवालों के उत्तर बहुत आसान है, बस कमी है तो आंकडों की. आप आंकड़े ले आइये हम जवाब देते हैं :-) वैसे आंकडें न भी मिलें तो थियोरी तो दी ही जा सकती है तो चलिए कुछ साधारण बातों की चर्चा कर लेते हैं. यह मानते हुए की आंकड़े उपलब्ध है. वैसे इस प्रकार का काम खूब होता है आजकल. जैसे मान लीजिये रेडिफ.कॉम खोला आपने. हर एक विजीट और क्लिक की अनाल्य्सिस की जाती है. इस बात की भी अनाल्य्सिस की जाती है कौन से ऐडवटाइज्मेन्ट ज्यादा क्लिक होते हैं? और कैसी हेडलाइनें ज्यादा पढ़ी जाती है. अब रेडिफ.कॉम की घर की खेती है... सारे आंकड़े होते हैं उनके पास हमें आंकडें मिलेंगे कहाँ से?

इन सब में डाटा माइनिंग,पैटर्न मैचिंग और सांख्यिकी का खूब इस्तेमाल होता है. मेरे कई दोस्त इस तरह के काम भी करते हैं.

अब मान लीजिये की सारा आंकडा उपलब्ध है तो उसमें ट्रेंड निकालना बड़ी बात नहीं होती. और उससे कई तरह की जानकारी निकाली जा सकती है. और फिर जरुरत के हिसाब से मॉडल में सुधार भी किया जा सकता है. कुछ प्राथमिक जानकारी तो ऐसे ही मिल जायेगी जैसे:
- कितने प्रतिशत पोस्ट ऐसे हैं जिन पर टिपण्णी है.
- हर पोस्ट पर औसत कितनी टिपण्णी आती है (इसके साथ ही माध्यिका(median) और बहुलक(mode) भी निकाला जा सकता है).
- औसत अंतराल जिन पर टिपण्णी आती है किसी ब्लॉग पर.
- टिपण्णी की लम्बाई (उसका औसत, मध्यिका, मानक विचलन(standard deviation) इत्यादि)

अब वितरण भी निकाला जा सकता है... मेरे हिसाब से अगर टिपण्णीयों की संख्या का वितरण (distribution) निकाला जाय तो कुछ इस तरह का आना चाहिए. यहाँ एक्स-अक्सिस पर टिपण्णीयों की संख्या तथा वाय-अक्सिस पर ब्लोगों की संख्या है. इसे लम्बी पुँछ का वितरण (Long tail distribution) भी कहा जाता है.बात साफ़ है ज्यादा टिपण्णी वाले ब्लोगों की संख्या कम है और कम या फिर बिना टिपण्णी वाले ब्लॉग की संख्या ज्यादा. अगर टिपण्णी की लम्बाई ले तो भी ऐसा ही वितरण आना चाहिए यानी किसी ब्लॉग पर लम्बी टिपण्णी वाले पोस्ट कम और छोटी टिपण्णी वाले पोस्ट ज्यादा होंगे. (यहाँ एक्स-अक्सिस पर टिपण्णी की लम्बाई और वाय-अक्सिस पर पोस्ट की संख्या).अगर एक बार वितरण का अनुमान हो गया तो फिर कई सूत्र हैं जानकारी निकालने के लिए. अब इसमें कुछ आउटलायर भी होंगे, जैसे मान लीजिये किसी ने टिपण्णी करना ही डिसेबल कर दिया हो. या फिर ऐसे जिन्हें खूब टिपण्णी मिलती हो. वैसे बिना आंकडों के भी ऐसे आउटलायरों को तो हम जानते ही हैं :-)

अब आगे बढ़ते हैं अगले सवालों की तरफ़ अगर हम ब्लॉग पर आने वालों की संख्या तथा टिपण्णी की संख्यां के बीच सहसंबंध (correlation) निकाल लें तो ये भी बड़े काम की जानकारी होगी, इससे ये पता चलेगा की किसी ब्लॉग पर आने वाले लोग टिपण्णी करते हैं या नहीं (हिट्स बढ़ा लेने की लिए ब्लॉग पर कीवर्ड या विवादित शब्द डाले जा सकते हैं, पर इससे टिपण्णी की संख्या नहीं बढाई जा सकती !) अब इसमे भी वितरण निकालने पर आउटलायर निकाले जा सकते हैं, वैसे जिनपर लोग आते तो हैं पर टिपण्णी नहीं करते (इसका कारण मोडरेशन भी हो सकता है). और ऐसे भी जिन पर लोग तो कम आते हैं पर उस हिसाब से टिपण्णी ज्यादा ऐसा हिन्दी ब्लोग्स में अक्सर देखने को मिलता हैं जहाँ लोग एक मित्र मंडली की तरह ब्लॉग पढ़ते हैं और जो भी आता है एक टिपण्णी चटका जाता है. तो लोकप्रियता का बेहतर मापदंड केवल टिपण्णी या केवल ब्लॉग विजीट न होकर उनके बीच का सहसंबंध भी हो सकता है. अब ऐसा भी होता है की किसी एक ब्लॉग में कुछ पोस्ट ओउलायर होते हैं... इनको अलग करके इनमे पैटर्न निकाला जा सकता है. पैटर्न निकालने में एक उदहारण देना चाहूँगा मान लीजिये की हम देखते हैं की किसी ब्लॉग पर आई कुल टिपण्णीयों में कितने 'साधुवाद', फिर 'सहमत हूँ आपसे', 'धन्यवाद इस पोस्ट के लिए', 'रोचक जानकारी' जैसे हैं. इनकी संख्या तथा अन्य टिपण्णीयों की लम्बाई पर मॉडल बनाए जा सकते हैं. इसके अलावा इस बात की भी जांच की जा सकती है की कितने बजे छपने वाले पोस्ट पर कितनी टिपण्णी आती है. (इसके लिए एक ही ब्लॉग के पोस्ट के छपने का समय और आई टिपण्णीयों का सम्बन्ध भी मिल सकता है) बहुत तरह का गणित लगाया जा सकता है, जरुरत है तो सिर्फ़ आंकडों की !

आगे जिस सवाल की चर्चा होनी है वो गणित के एक हलके सवाल से शुरू हुआ और गणित का सबसे कठिन सवाल बन गया, इतना आसन की छठी कक्षा के छात्र को समझ में आ जाय और इतना कठिन की ४०० सालों तक कोई गणितज्ञ ना हल कर पाया. इतिहास के सबसे बड़े-बड़े गणितज्ञों ने हाथ आजमाया... क्या हुआ जानते हैं जल्दी ही.. !

~Abhishek Ojha~

गणित के कुछ वास्तविक प्रयोग (बातें गणित की भाग... V)

आज गणित के कुछ ऐसे प्रयोग जिनसे मैं ख़ुद जुडा हूँ, जी हाँ कुछ ऐसे प्रयोग जिनपर मैंने काम किया... अर्थशास्त्र, मार्केटिंग, मनोविज्ञान और इंजीनियरिंग जैसे कुछ क्षेत्रों से बातें होगी, फुटबॉल और क्रिकेट जैसे खेल आपको पसंद हैं तो उनका भी जिक्र भी आ जायेगा और अगर आपको लगता है की मैच देखना समय की बर्बादी है तो वो भी जोड़ लेंगे... कहीं आपको ऐसा तो नहीं लग रहा है की ये सब गणित में कहाँ से आ गया, अब वास्तविक प्रयोग है तो वास्तविकता ही ज्यादा होगी ना ! अगर आप इससे आगे नहीं पढ़ रहे तो आपको बताता चलूँ की जल्दी ही गणित के सबसे रोचक सवाल के इतिहास और उससे जुड़े रोचक तथ्यों पर अगली पोस्ट आने वाली है (अगर ये पोस्ट दो भागों में नहीं बटी तो) पर आगे पढने से डरने की जरुरत नहीं है... सब कुछ समझ में आने की गारंटी मेरी !

1. बात की शुरुआत राजनीति और उर्जा से... तेल की कीमतों और न्यूक्लियर डील से तो आप सब परिचित हैं ही, अब एक और विकल्प भी आप अखबारों में देखते ही होंगे ईरान-पकिस्तान पाइपलाइन की... ईरान से पाकिस्तान होते हुए भारत तक गैस लाने के लिए पाइपलाइन बनाने की. अब गणित लगाना था की कौन-कौन से विकल्प हैं भारत के पास... कौन सा विकल्प महंगा पड़ेगा और कितना... चलिए अब इस प्राकृतिक गैस के बारे में भी जान लेते हैं... दो मुख्य तरीके होते हैं इसे एक जगह से दुसरे जगह ले जाने के, पहला गैस पाइपलाइन और दूसरा टैंकरयुक्त पानी के जहाजों से. तो फिर पाकिस्तान को बीच में लाने की जरुरत ही क्या है? टैंकर से ही ले आते हैं... पर गणित कुछ और कहता है... जब हम खर्च की बात करते हैं तो पता चलता है की एक ख़ास दुरी तक से गैस लाने में पाइपलाइन की गैस बहुत सस्ती पड़ती है वहीँ उस दूरी से ज्यादा दूरी से गैस लानी हो तो टैकर सस्ते पड़ते हैं. खर्चे कई तरह के होते हैं, कुछ खर्चे दोनों तरीकों में होते हैं जैसे गैस को निकलना और उसे उपयोगी बनाना, जमीन या समुद्र से निकलने वाली गैस में कई सारे अवांछनीय पदार्थ भी होते हैं... कई बार इन अवांछनीय पदार्थों को जमीन के अन्दर वापस डालना पड़ता है... इसे वापस डालते समय भी इससे प्रेसर बनाया जाता है ताकि और गैस जमीन के अन्दर से आसानी से निकाली जा सके. टैंकर का इस्तेमाल करना हो तो गैस को पहले द्रव में परिवर्तित करना पड़ता है, उसके बाद टैंकरों का खर्च अलग, तो क्या पाइपलाइन एक बार बना दी तो गैस भेजते रहो? नहीं ऐसा नहीं है... पाइपलाइन में उपयुक्त प्रेशर बनाए रखने के लिए थोडी-थोडी दूर पर कम्प्रेसर लगाने पड़ते हैं, और उनका खर्च अलग से, उनके लिए उर्जा भी अलग से... दोनों ही तरीकों में मेंटेनेंस जैसे खर्च होते ही हैं. जैसे दूरी के हिसाब से टैंकर बेहतर हो जाता है वैसे ही कांट्रेक्ट की अवधि के हिसाब से भी होता है... अगर लम्बी अवधि का कांट्रेक्ट हो तो पाइपलाइन सस्ता पड़ता है और कम अवधि का हो तो द्रवित प्राकृतिक गैस के टैंकर सस्ते होते हैं. पाइपलाइन भी जमीन के अलावा समुद्र में भी हो सकती है... उसके लिए टेक्नोलॉजी और खर्च दोनों चाहिए. इस तरह इन सारी चीज़ों का ध्यान रखते हुए हमने मॉडल बनाया और फिर ग्राफ्स और अन्तिम कीमत निकलने के लिए सूत्र. पाइपलाइन वाला फार्मूला थोड़ा जटिल हो गया क्योंकि कम्प्रेसर के लिए मेकेनिकल इंजीनियरिंग की मदद लेनी पड़ी.

2. अब बात करते हैं प्रोसेस मोडेलिंग की... ये काम बहुत रोचक था इसमें साधारण ओपरेशन रिसर्च से लेकर मनोविज्ञान तक का इस्तेमाल होता है, इसमें ये देखना था की किसी प्रोजेक्ट को पुरा करने वास्तविक रूप में कितना समय लगेगा, इसके लिए प्रोजेक्ट का पूरा आंकडा होना चाहिए और हर काम को कौन आदमी करेगा और उसकी योग्यता क्या है ये सब होना चाहिए, इसमें बहुत सारी बातें ध्यान में रखी गई जैसे मान लीजिये फूटबाल या क्रिकेट का वर्ल्ड कप चालु हो गया तो फिर उसका क्या असर होगा? इस काम के विशेषज्ञ स्टैनफोर्ड विश्वविद्यालय के प्रोफेसर रेमंड लेविट के विडियो लेक्चर को खूब सुना... लेक्चर सुनता और विद्यार्थियों को पढाता भी :-) अपने से बड़ों को पढाना, कई बार अपने गाइड को भी पढाता :-) इससे अच्छा और क्या हो सकता है !

3. एक और रोचक प्रोजेक्ट के बारे में आपको बता दूँ... मान लीजिये की आप किसी भीड़-भाड़ वाले स्टेशन पर खड़े हैं और आग लग जाए तो आप क्या करेंगे? भागेंगे... किस दिशा में भागेंगे? निकास की तरफ़... आकस्मिक भय (पैनिक) की हालत में अगर सब भागने लगें तो क्या हो? स्टेशन तो ये सोच के बनाया नहीं गया था... अब मान लीजिये की इस हिसाब से स्टेशन के भवन में बदलाव लाना है, तो कैसे लाया जाय ताकि पूरा भवन गिराना न पड़े... इसके लिए गणित को याद किया गया और फिर कम्प्यूटर साइंस को... और बन गया ये प्रोडक्ट, इस काम करना भी खूब रोचक रहा और हमने ज्यूरिक रेलवे स्टेशन को ओप्टिमाइज किया.

4. आपने थ्री डाइमेन्सन तो सुना ही होगा पर कभी फ़ोर डाइमेन्सन सुना है? जी हाँ एक समय भी जोड़ दीजिये... फ़ोर डाइमेन्सन में किसी प्रोजेक्ट का ओप्टिमाइजेसन करने का काम जेनेटिक अल्गोरिथम से... छोडिये नाम से ही भारी हो रहा है... इस काम को करने में भी बहुत मज़ा आया.

5. अब चलिए थोड़ा एन्सुरेंस एजेंट और लोन वसूली को आराम दिया जाय, जी हाँ ये पता करना की कौन आदमी लोन और प्रीमियम सही टाइम पर देगा और कौन देर से करेगा... उस हिसाब से उसी एरिया में एजेंटों को भेजा जाय तो कितनी अच्छी बात होगी... और पैसे की बचत भी होगी, इस काम को करने के लिए कई मॉडल हैं पर ये समय के साथ बदलते नहीं ! मान लीजिये किसी की माली हालत बीच में ख़राब हो गई तो? इसलिए हमने हर कलेक्शन के बाद मॉडल में सुधार किया (यह बेसियन इकोनोमेट्रिक्स का एक प्रयोग था, पहले ऐसे कम्प्यूटर नहीं थे जो इतना बड़ा-बड़ा हिसाब कर सकें इसलिए पहले इस विधा का उपयोग नहीं हो पाता था), आप इसे डायनामिक मॉडल कह सकते हैं।

6. थोड़ा तेल-साबुन बेचने का भी प्रयास किया, कनाडा के एक मुहल्ले से आंकडा लाया गया और अब पता ये करना था की किस तरह की आय वाली जगह पर कैसा डिटर्जेंट बेचा जाय और कौन सा केचप... सीधी सी बात है समाज का जो वर्ग निरमा खरीदता है वो सर्फ़ एक्सेल नहीं... (इसे मार्केट सेगमेंटेशन भी कहा जाता है, इस पर भी जो स्थायी मॉडल हैं उन पर कुछ सुधार का काम किया).

7. अब सब बेच लिया तो कुछ खरीदने की बात भी हो जाय... तो भारत में गाड़ियों की विक्री किस तरह बढ़ी है, कितना बढेगी... इस पर भी कुछ दिन काम किया...

8. और अंत में मेरी थीसिस... जो थोडी ज्यादा गणितीय है इसीलिए इतना बता दूँ की यह नेटवर्क फ्लो पर आधारित था... नेटवर्क किसी भी चीज़ का हो सकता है... मान लीजिये रेल या सड़क का पूरा एक नेटवर्क है... एक से दूसरी जगह समान भेजना है... इसको कैसे आसानी से एक जगह से दूसरी जगह भेजना है ताकि खर्च और समय बचे... ज्यादा से ज्यादा सामान भेजा जा सके, इस काम के लिए कई अल्गोरिथम है... पर हमारा काम इस बात का था की अगर कम्प्यूटर इस सवाल के लिए एक घंटे लेता है तो कैसे इसे कम समय में किया जाय... हमने नया अल्गोरिथम तो नहीं दिया. हाँ ऐसे अल्गोरिथम अनुमान के साथ चालु किए जाते हैं और सही उत्तर की जगह जाकर जाते हैं, हमारे काम से ऐसे अनुमान लगाए जा सकते हैं जो कई बार ९०% तक कम समय में सवाल हल कर देते हैं. ये वैसे ही है जैसे मान लीजिये धुंध में आपको दिखाई नहीं दे रहा है और आपको पहाड़ की ऊंचाई पर चढ़ना है... आप अपने हिसाब से एक ऊँचे जगह पर पहुच कर यात्रा प्रारम्भ करेंगे और जो सबसे ऊँचा दिखाई देगा वहां तक पहुचते जायंगे... इस प्रकार कुछ देर के बाद आप अपने आपको सबसे ऊँची जगह पर पायेंगे... अब आप पहले से ही ऊंचाई पर हैं तो उसी समय पता लग जायेगा की इससे ऊपर कुछ नहीं है... हम भी ऐसे ही ऊँची जगह का काफ़ी हद तक (८०% स्थितियों में) पता लगाने में सफल रहे. चलिए बहुत हो गया... अगले पोस्ट में जैसा की मैंने कहा सबसे रोचक सवाल पर चर्चा होगी... उस पर बनी एक डॉक्युमेंट्री भी बहुत प्रसिद्द हुई... और भी छोटे-मोटे प्रोजेक्ट हैं, पर पोस्ट वैसे ही लम्बी होती जा रही है... इसलिए बस इतना ही !

अलग अलग प्रोजेक्ट इन जगहों पर किए गए..
1. IIM Bangalore, December 2004
2. i4Ds, Switzerland, May-July 2006
3. i4Ds, Switzerland, May-July 2005 (Known as aec-ii at that time)
4. i4Ds, Switzerland, May-July 2006
5. IIM Bangalore, December 2005
6. IIM Bangalore, December 2005
7. IIT Kanpur, May-July 2004
8. IIT Kanpur, Aug 2006-May 2007

अगर गलती से किसी के बारे में और जानने की इच्छा हो तो जरूर पूछें.

---

इसे एक ओवरव्यू की तरह ही लिया जाय... इस सप्ताह मुंबई जाना पड़ा और भी कई सारे काम आ गए, इस श्रृंखला को जारी रखने के लिए ये पोस्ट लिख डाली. इन विषयों पर विस्तृत चर्चा अलग-अलग पोस्ट में की जायेगी. (यह फैसला द्विवेदीजी और मसिजीवी जी की टिपण्णी को ध्यान में रखते हुए लिखा गया है)

---

~Abhishek Ojha~