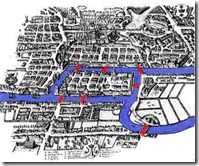
कोनिसबर्ग के पुलों वाली पहेली और टोपोलोजी की शुरुआत

कोनिसबर्ग के पुलों वाली पहेली एक सरल और रोचक ऐतिहासिक पहेली है. ये गणित की उन पहेलियों में से है जिन्हें समझना बिल्कुल ही आसान था, पर हल करना थोड़ा मुश्किल. कहते हैं टोपोलोजी की विचारधारा का जन्म इसी पहेली से हुआ. यह पहला सवाल हैं जहाँ पर टोपोलोजी के निशान देखे जा सकते हैं. यही नहीं गणित (और कम्प्युटर साइन्स) की एक प्रसिद्ध शाखा ग्राफ थियरि का विकास भी इसी पहेली से शुरू हुआ. तब जर्मनी के कोनिसबर्ग शहर जो अब कालीनीनग्राद  के नाम सेजाना जाता है और अब रूस में स्थित है के प्रेगेल नदी से बने द्वीप और नदी पर बने सात पुलों ने एक पहेली को जन्म दिया. हालांकि द्वितीय विश्व युद्ध में इनमें से दो पुल ध्वस्त हो गए और उन पुलों में से अब बस पाँच (इन पाँच में से दो पुल उस समय के हैं, बाकी फिर से बनाये गए हैं) बचे हैं. कोनिसबर्ग के तब की तस्वीर का रेखाचित्र और अब के गूगल अर्थ की तस्वीर से तुलना की जा सकती है.

  

कोनिसबर्ग तब व्यापार का केंद्र हुआ करता और ये पुल शहर के अलग-अलग हिस्सों में जाने के लिए इस्तेमाल किए जाते. कोनिसबर्ग के किसी घुमंतू खुराफाती व्यक्ति के दिमाग में ये सवाल आया कि क्या किसी एक जगह से शुरू होने वाली ऐसी यात्रा संभव है जिसमें एक ही यात्रा में इन सातों पुलों को एक और बस एक ही बार पार किया जाय और उस जगह पर वापस आया जाय जहाँ से यात्रा शुरू की गयी थी. ना तो किसी पुल को दुबारा पार करना पड़े और ना ही आधा.

अब पहेली तो बन गयी पर ऐसा रास्ता कोई नहीं ढूँढ पाया. ना ही कोई ये सिद्ध कर पाता कि ऐसा संभव नहीं है. अगर आपको याद हो तो बचपन में हमसे भी कुछ होशियार बच्चे कहते कि बिना कलम उठाये एक विकर्ण सहित वर्ग बनाकर दिखाओ. अब बनाने की कोशिश तो हम सभी करते और अंत में कहते नहीं हो रहा ! कुछ ऐसी ही हालत कुछ वर्षों तक  रही होगी कोनिसबर्ग में भी. फिर किसी ने 1736 में ये पहेली तब के प्रसिद्ध गणितज्ञ ओयलर को लिख भेजा. ओयलर सेंट पिटसबर्ग में रहते थे. और उस समय गणित के अलावा यांत्रिकी, भौतिकी और खगोलीय विषयों पर भी काम करते थे. अब इतने मशहूर व्यक्ति थे तो जाहिर है व्यस्त भी रहते थे. कहते हैं उस दौरान वो औसतन सप्ताह में एक शोध पत्र छापा करते. ओयलर को ये सवाल पहले तो बहुत हल्का और बेकार सा लगा पर फिर उन्होने स्वयं एक पत्र में लिखा 'ये मामूली सा सवाल है पर फिर भी मुझे यह समय व्यतीत करने लायक लगा क्योंकि ज्यामिति, बीज गणित और अंक गणित से इसे हल कर पाना संभव नहीं लगता. ' ओयलर ने इस सवाल को व्यापक बनाकर हल किया और यह दिखाया कि किन हालतों में (कितने पुल हो तो) ऐसी यात्रा संभव है. उन्होने यह भी दिखाया कि 7 पुल वाले  मामले में ऐसी यात्रा संभव नहीं.
गौर करने की बात ये है कि इस पहेली में कौन सा पुल किस से कितनी दूरी पर है और किस पुल की लम्बाई कितनी है यह मायने नहीं रखता. संभवतः गणित का यह पहला ऐसा सवाल था जिसमें ज्यामिति जैसी स्थिति होते हुए भी नापने या अंकों की बात ही नहीं थी ! साथ ही यह भी मायने नहीं रखता था कि एक पुल से दूसरे पुल तक जाने का रास्ता सीधा था या टेढ़ा-मेढ़ा. ओयलर ने इसे ग्राफ थियरि से हल किया, इसे हल करने के सिलसिले ने ही ग्राफ थियरि को जन्म दिया और फिर आगे चल कर इन अवधारणाओं पर ही टोपोलोजी का जन्म हुआ. बाद के मशहूर ट्रावेलिंग सेल्समैन जैसे सवाल भी एक तरह से इसी श्रेणी में आते हैं. टोपोलोजी में एक जैसे सवालों/वस्तुओं/समुच्चयों का एक समूह होता है. जैसे यहाँ एक जगह से दूसरी जगह जाने के रास्ते के बीच की दूरी और सीधा-टेढ़ा होना माने नहीं रखता वैसे ही वहाँ एक गोले और घन में फर्क नहीं होता क्योंकि एक को पीटकर दूसरा बनाया जा सकता है. टोपोलोजी के इस सिद्धांत की चर्चा अगले पोस्ट में. 
गूगल ने इस प्रसिद्ध पहेली से जुड़ी प्रेगेल नदी के नाम पर ही अपने एक ग्राफ कम्प्यूटिंग का नाम प्रेगेल रखा है.
और ये रही ओयलर के आरिजिनल पेपर से एक तस्वीर: 

__________________________________________
पोस्टोपरांत अपडेट: (अभय तिवारी जी की टिपण्णी के बाद)
ओयलर का हल:
ओयलर ने इस पहेली को ग्राफ में परिवर्तित किया और जैसा कि मैंने ऊपर कहा इस ग्राफ में रेखाओं का सीधा-टेढ़ा होना और बिन्दुओं के बीच की दुरी मायने नहीं रखती. इस ग्राफ में बिंदु जमीन और सात रेखाएं सात पुलों को दर्शाती हैं. ओयलर ने कहा कि पहेली के हिसाब से अगर एक रास्ता ढूँढना है तो यात्रा करते समय बीच में आने वाले सारे बिन्दुओं पर एक आने का और एक जाने का रास्ता होना चाहिए. इस हिसाब से सारे बिन्दुओं पर रेखाओं की संख्या सम होनी चाहिए. केवल २ बिन्दुओं पर जहाँ से यात्रा शुरू हो और जहाँ ख़त्म हो केवल वहीँ विषम संख्या में रेखाएं हो सकती है. और अगर यात्रा जहाँ से शुरू करनी है वहीँ ख़त्म भी तो फिर सारे ही बिंदुओं पर रेखाओं की संख्या सम होनी चाहिए. पर इस ग्राफ में सभी बिन्दुओं पर विषम संख्या में रेखाएं हैं (३ और ५). इसलिए पहेली के हिसाब से यात्रा संभव नहीं है !
__________________________________________

~Abhishek Ojha~