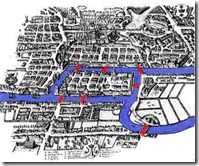
कभी आपने सोचा है एक रंगीन नक्शे (मानचित्र) में कितने तरह के रंग प्रयोग किए जाते हैं? वैसे तो चाहे जितनी मर्जी इस्तेमाल किए जा सकते हैं लेकिन 1852 में एक नक्शे को रंगते हुए फ्रांसिस गुथरिए नामक एक वनस्पतिशास्त्री और गणितज्ञ के दिमाग में ये सवाल आया कि कम से कम कितने रंगों के इस्तेमाल से कोई भी नक्शा बनाया जा सकता है ताकि कोई भी दो पड़ोसी देशो को एक ही रंग में ना रंगना पड़े? देशों के आकार-प्रकार और हर देश के लिए पड़ोसी देशों की संख्या जो भी हो उन्होने अटकलबाजी करते हुए एक अनुमान लगाया कि इस सवाल का उत्तर चार रंग है. और चार रंग ही पर्याप्त हैं ऐसे किसी भी नक्शे को बनाने के लिए. इस अनुमान ने चार रंगों वाले कंजेक्चर को जन्म दिया.
गणित में अटकलबाजी का बड़ा महत्त्वपूर्ण स्थान है. अनुमान, अनुभव और अंतर्ज्ञान के आधार पर गणितज्ञ कोई बात कह देते हैं. जब तक ये बात सही या गलत सिद्ध नहीं हो जाती तब तक इसे अटकलबाजी ही तो कहेंगे ! तो इन्हें तब तक कंजेक्चर कहा जाता है, सिद्ध हो जाने के बाद ये कंजेक्चर प्रमेय हो जाते हैं.
फ्रांसिस के अनुमान के बाद सौ वर्षों से अधिक तक यह सवाल अनुमान ही बना रहा. चार रंग वाले सवाल (फोर कलर प्रोबलम) के नाम से प्रसिद्ध यह टोपोलोजी के सबसे प्रसिद्ध और ऐतिहासिक सवालों में से एक है. बाकी सवालों की ही तरह इसे भी हल करने के प्रयास होते रहे और कई लोगों ने इसे साबित भी कर दिखाया. इन कई लोगों के प्रमाण कई वर्षों तक मान्य भी रहे. पर कुछ सालों बाद इनमें गलतियाँ ढूँढ ली गयी. ऐसे ही एक प्रमाण को गलत साबित करते हुए 1890 में पार्सि जॉन हेवूड ने एक नया सिद्धांत दिया जिसमें उन्होने यह साबित किया कि पाँच रंगों से ऐसे नक्शे बनाना संभव है. पर वो ये नहीं दिखा सके कि चार रंगों में ही संभव है या नहीं ! तो मूल सवाल अभी भी बना रहा.
इस सिलसिले में ग्राफ थियरि और टोपोलोजी का खूब विकास हुआ. ग्राफ रंगने से जुड़े अनगिनत सिद्धांत और सवालों का जन्म हुआ. ग्राफ थियरि में इस सवाल को इस तरह देखा जाता है: हर देश को एक बिन्दु से निरूपित किया जाता है और हर पड़ोसी देश को एक रेखा से जोड़ दिया जाता है. फिर सवाल ये हो गया कि कितने रंग चाहिए जिससे एक रेखा से जुड़े कोई भी दो बिन्दु एक ही रंग में ना रंगे हो? वैसे तो लगता है... ठीक है रोचक सवाल है. लेकिन इसका क्या उपयोग है? इस सवाल का बड़ा व्यापक उपयोग है... जैसे टेलीकॉम कंपनियां अपना नेटवर्क डिजाइन करते समय इसका इस्तेमाल कुछ इस तरीके से करती हैं: कम से कम कितने ट्रांसमीटर में काम हो जायेगा और फिर उतने ट्रांसमीटर से नेटवर्क डिजाइन कैसे किया जाय?
हाँ तो ये रंगों का सवाल कंजेक्चर बना रहा और अंततः 1976 में इलियोनोई विश्वविद्यालय के वोल्फगैंग हेकेन और केनेथ एपेल ने घोषणा की ये चार रंगों वाला सवाल अब चार रंगों वाले प्रमेय के नाम से जाना जायेगा. यानि उन्होने इस कंजेक्चर को सिद्ध कर देने की घोषणा की. पर समस्या अभी गयी नहीं और इस हल ने एक नए विवाद को जन्म दिया. कई गणितज्ञों ने इस हल को मानने से इंकार कर दिया. इस हल में गणित के अलावा कंप्यूटर की मदद ली गयी. इस सवाल को हल करते हुए अंत में 1476 ऐसी अवस्थाएँ बची जिन्हें अगर एक-एक करके जाँच लिया जाय तो ये हल पूर्ण हो जाता. लेकिन इस जाँच में इतनी गणनाएँ थी कि इन्हें कागज-कलम और इंसानी दिमाग-समय में करना असंभव था. दोनों गणितज्ञों ने इस हिस्से को कम्प्युटर जनित अलगोरिथ्म्स से जाँच लिया (कम्प्युटर पर भी इन्हें जाँचने में हजारो घंटे लगे). पर कुछ गणितज्ञों की आपत्ति थी कि अगर कुछ गणनाओं में कहीं कोई गलती हुई तो? पर यह लगभग मान लिया गया कि फ्रांसिस का अनुमान सही था और चार रंग ही पर्याप्त हैं. तब से अब तक कई परिष्कृत प्रमाण दिये गए इस सवाल के. 2005 में माइक्रोसॉफ़्ट के जोर्जेस गोथिएर और इनरिया के बेंजामिन वर्नर ने इस प्रमेय का एक नया प्रमाण दिया पर वह भी कम्प्युटर आधारित ही है. पर इस प्रमाण में एक-एक करके जाँचने वाला चरण नहीं है. यह प्रमाण फंकशनल प्रोग्रामिंग लैंगवेज़ और कैलकुलस ऑफ इंडक्टिव कंस्ट्रक्शन पर आधारित इंटरैक्टिव थियोरम प्रूवर पर आधारित है.
बिना कम्प्युटर की मदद के इस प्रमेय का अभी भी कोई प्रमाण नहीं है. इस प्रमेय के हल के बाद कम्प्युटर वाली पद्धति का और भी कुछ सवालों के हल में इस्तेमाल हुआ है. वैसे ये पद्धति अभी भी विवादास्पद बनी हुई है !
~Abhishek Ojha~
--
इस पोस्ट के लिए उन्मुक्तजी का धन्यवाद. उन्होने पिछली पोस्ट पर की गयी टिपण्णी में इस सवाल पर लिखने का सुझाव दिया था.